Calculus and optimization

1.2. Calculus and optimization#

1.2.1. Derivative#

1.2.1.1. Derivative#

1. Đạo hàm tại 1 điểm

Độ dốc slope của 1 điểm là độ lớn đường tiếp tuyến với hàm F(x) tại điểm đó.
Đạo hàm giúp tính toán sự thay đổi của Y tại 1 điểm X cụ thể (thay vì tính toán sự thay đổi của Y từ Y1 –> Y2 khi X1 –> X2)
Trong bài toán ML, X là weight còn Y là hàm Loss

–> quá trình học tạo ra sự thay đổi weight, với mỗi weight thì sẽ có sự thay đổi của Loss. Sự thay đổi của weight sẽ cần phù hợp với độ lớn của sự thay đổi của hàm Loss. Hơn nữa, do cần hạn chế sự thay đổi quá nhanh của hàm loss nên bước nhảy cần nhỏ, yêu cầu lượng data lớn để học

2. Hàm Loss

Hàm loss thay đổi ít khi train qua các obs tương đồng nhau, thay đổi lớn khi gặp các quan sát khác biệt hoặc noise. Chuẩn hoá giúp giảm sự khác biệt của nóie trong bộ dữ liệu.
Các weight của model thay đổi theo chiều hướng làm hàm Loss nhỏ dần, slope càng lớn thì learning-step càng nhanh, khi slope gần tiến về 0 thì bước nhảy càng bé.
Với hàm Loss có nhiều điểm local minimum (slope = 0) thì cần:
- Điểm start-point tại nheièu vị trí khác nhau
- Random/shuffer data
- Sử dụng momentum

3. Chain Rule

Quy tắc chuỗi là một công thức để tính các đạo hàm của 1 hàm tổng hợp. Hàm tổng hợp là hàm bao gồm các hàm khác bên trong.

Ví dụ: L(w) = C(a(z(w)))

Trong mạng neural network thì mỗi layer chứa 1 hàm $z$ và 1 hàm activate $a$. Khi đó, để tính được đạo hàm của hàm Loss ($C_0$) thông qua $w$ thì ta tính đạo hàm theo công thức trên

4. Partial derivative - đạo hàm theo nhiều chiều

Trên tập dữ liệu nhiều chiều x, y có hàm F(x,y), partial derivative là các đạo hàm theo từng chiều x, y của hàm F
Gradient decent của F(x,y) là tổng hợp các vector partial từ các hướng thành phần x,y
Mulvarivate chain rule = tổng các univariate chain rule của từng chiều thành phần.

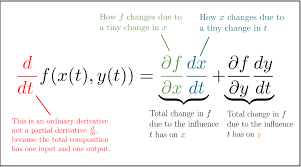
5. Second derivative

Đạo hàm bậc 2 giúp xác định điểm cực trị là min hay max, thể hiện mức độ thay đổi của biến thiên f(x) khi x thay đổi

1.2.1.2. Jacobian & Hessian matrix#

1. Jacobian matrix Ma trận kích thước m.n thể hiện đạo hàm thành phần của m hàm f theo n giá trị x —> trong xử lý ảnh thì jacobian giúp tìm các đường giao màu

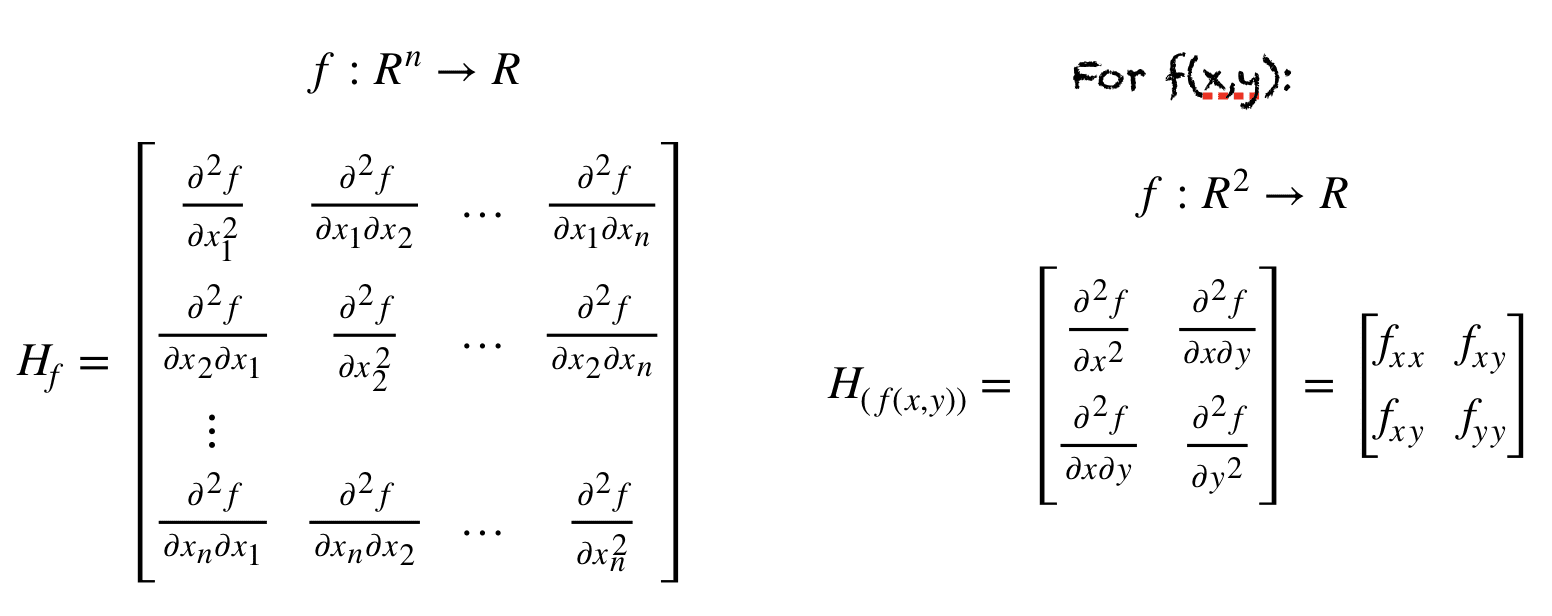
2. Hessian matrix Ma trận đạo hàm bậc 2 của 2 biến x,y tác động đến hàm f –> trong xử lý ảnh thì hessian giúp tìm các điểm giao cắt

1.2.2. Activate function#

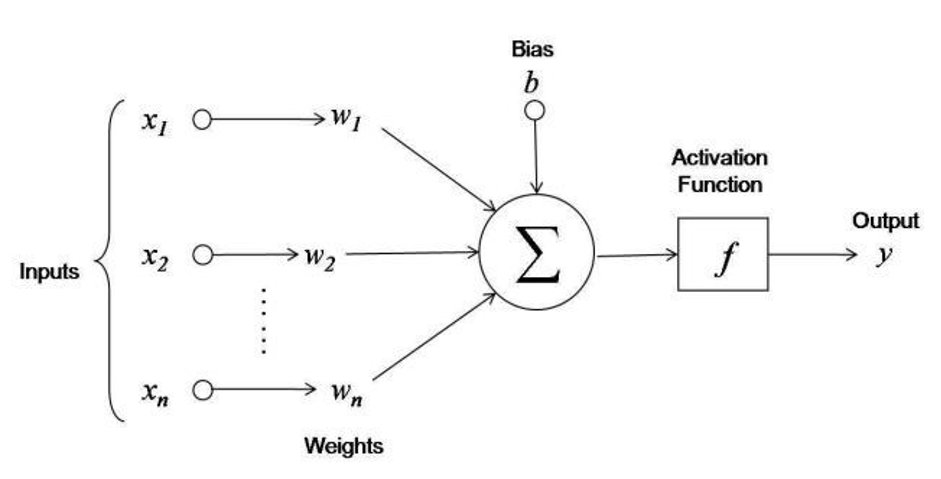
AF giúp biến đổi non-linear các hàm ban đầu để phù hợp với thực tế, do hàm trước AF chỉ là tổ hợp tuyến tính
AF giúp hạn chế tác động và kiểm soát những value lớn
Trong việc learn của model, cần tránh các TH:
- Học bùng nổ: hàm loss rất lớn khi có nhiễu
- triệt tiêu thông tin: gradient trở nên rất bé và gần như ko học được gì

Lựa chọn activate function

Thông thường SELU > ELU > leaky ReLU (và các biến thể) > ReLU > tanh > logistic.
Quan tâm tới runtime, prefer leaky ReLU.
PReLU if you have a huge training set
Bài toán hình ảnh: ưu tiên hàm ReLU
NLP: sigmoid, Tanh, Ramp

For regression problems(Only 1 neuron, multiple inputs, real-world outputs), a linear activation function must be used.
For multi-class classification problems, use Softmax at the output layer
For multi-label and binary classification problems, use the Sigmoid activation function.
Sigmoid and hyperbolic tangent activation functions must be never used in the hidden layers as they can lead to vanishing gradients.
For networks where unnecessary neurons need to turn OFF, use ReLU as the activation function because it also works as a dropout layer. In case there is confusion about which activation function, use ReLU.It is used in most CNN problems.
For deep neural networks having greater than 40 layers, use the swish activation function.

import numpy as np
import plotly.graph_objects as go
from tensorflow.keras import activations as af

def derivative_value(func , x, step=1e-10):
    return (func(x+step) - func(x)) / step

def plot_output_and_deriv(func, name = "", range_x = np.linspace(-5,5, 50)):
    fig = go.Figure()
    fig.add_trace(go.Scatter(x=x, y=[func(x) for x in range_x], mode='lines', name=name))
    if func is not None:
        y_deri = [derivative_value(func ,i) for i in x]
        fig.add_trace(go.Scatter(x=x, y=y_deri, mode='lines+markers', name='derivative of '+name))
    return fig.show(renderer = 'jpeg')

1.2.2.1. Unit step#

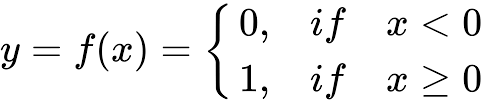
Mô tả: Input là toàn bộ số thực, trả về 1 nếu dương, trả 0 nếu âm
Đạo hàm: = 0
Pros: Đơn giản + dễ áp dụng
Cons: Đạo hàm = 0 nên không có tác dụng trong việc cập nhật trọng số
Usage: Thường áp dụng cho output layer thay vì hidden layer và áp dụng trong các bài toán binary classification

unitstep = lambda z: int(z>0 or z ==0) 
plot_output_and_deriv(unitstep, 'unitstep')

../../../_images/bde803377eda543be5ffcc021c0dcc394f53ecb38521a0513d2c6f4224c6c759.jpg

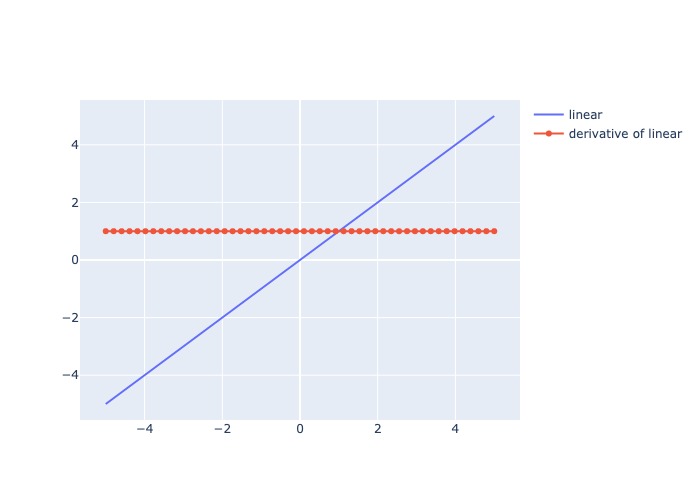
1.2.2.2. Linear#

\[y = aX + b\]

Mô tả: Trả output là 1 hàm linear của input
Đạo hàm: = constant
Pros:
- Range output rộng và không bị ràng buộc
- Chi phí tính toán thấp
- Không có hiện tượng biến mất gradient trong quá trình lan truyền ngược
Cons: Do đạo hàm cố định, tức giá trị update weight luôn cố định nên không phản ánh sự tương quan giữa X và y
Usage: Áp dụng cho các bài toán regression(univariate)

plot_output_and_deriv(af.linear, 'linear')

../../../_images/3f2546034554b51c284bccecdc62d55c83cc146bfe9301964dc808edeb23d0e9.jpg

1.2.2.3. Softmax#

\[\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}}\]

where $z_i$ is the $i$-th element of the input vector, and $k$ is the length of the vector

Mô tả: Chuẩn hoá các giá trị đầu vào về range (0,1) và có tổng bằng 1
Đạo hàm:
Pros:
- Phù hợp multi-class classification do có sum = 1
- Hàm liên tục và khả vi tại mọi vị trí, nên phù hơp với backpropagation
Cons:
- Tốn chi phí tính toán
- Chỉ dùng cho output layer
Usage:
- Áp dụng cho output là multi-class classification
- Chỉ áp dụng cho output layer

def softmax(x):
    ex = np.exp(x)
    sum_ex = np.sum( np.exp(x))
    return ex/sum_ex

af.softmax

<function keras.activations.softmax(x, axis=-1)>

1.2.2.4. Sigmoid#

\[{\displaystyle S(x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{e^{x}+1}}.}\]

Mô tả: Nhận input số thực và trả ra value trong (0,1), số input càng lớn, output càng gần 1, input càng bé thì output càng gần 0
Đạo hàm: Thay đổi và luôn dương, lớn nhất tại x = 0 và bé nhất khi x càng lớn hoặc càng bé
Pros:
- Weight luôn được cập nhật qua mỗi lần học
- Hàm liên tục và khả vi tại mọi vị trí, nên phù hơp với backpropagation
Cons:
- Tốn chi phí tính toán
- Không có tính đối xứng qua số 0 nên học các negative value sẽ ít hơn so với positive value
- vanishing gradient problem xuất hiện tại các điểm giá trị input quá lớn hoặc quá bé, khi đó derivative xấp xỉ 0
Usage:
- Áp dụng cho output là xác suất hoặc bài toán binary classification
- Nếu sử dụng cho multi-class classification thì tổng các xác suất sẽ khác 1, cần phải hiệu chỉnh lại bằng softmax

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

plot_output_and_deriv(af.sigmoid, 'sigmoid')

../../../_images/723dcfc25b73647444067ff0baa0302adb09e565928594960feeb9343a323cbd.jpg

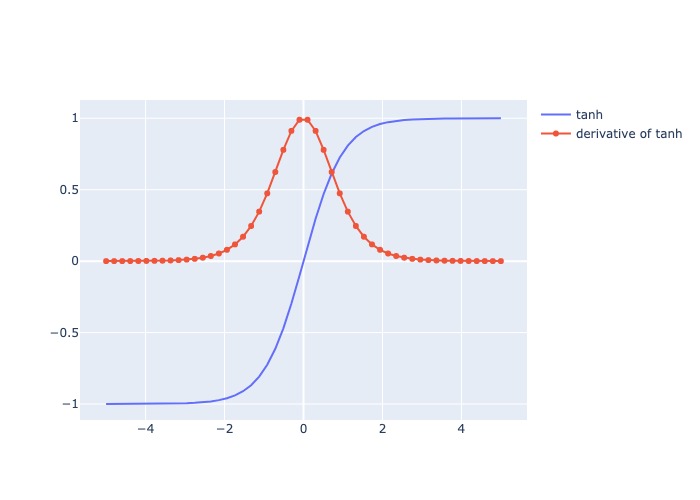
1.2.2.5. Hyperbolic Tangent (tanh)#

\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

Mô tả:
- Nhận input số thực và trả ra value trong (-1,1), số input càng lớn, output càng gần 1, input càng bé thì output càng gần -1
- Giống sigmod nhưng range output = (-1,1)
- Thường làm output tiến gần về/đến 0, tăng khả năng hội tụ
Đạo hàm: Thay đổi và luôn dương, lớn nhất tại x = 0 và bé nhất khi x càng lớn hoặc càng bé
Pros:
- Weight luôn được cập nhật qua mỗi lần học
- Hàm liên tục và khả vi tại mọi vị trí, nên phù hơp với backpropagation
- Có tính đối xứng qua số 0 nên học các negative value ngang bằng positive value, do đó hội tụ nhanh hơn sigmoid
Cons:
- Tốn chi phí tính toán
- vanishing gradient problem xuất hiện tại các điểm giá trị input quá lớn hoặc quá bé, khi đó derivative xấp xỉ 0
Usage:
- Thường áp dụng cho bài toán có nhiều output hoặc binary classification (sigmod thường áp dụng cho bài toán phân loại 2 output)

def tanh(z):
    ez = np.exp(z)
    enz = np.exp(-z)
    return (ez - enz)/ (ez + enz)

plot_output_and_deriv(af.tanh, 'tanh')

../../../_images/679bb7af1ab5ef2536ae7178b08c57186f4e5803e5b31bcc80541d5e48863bad.jpg

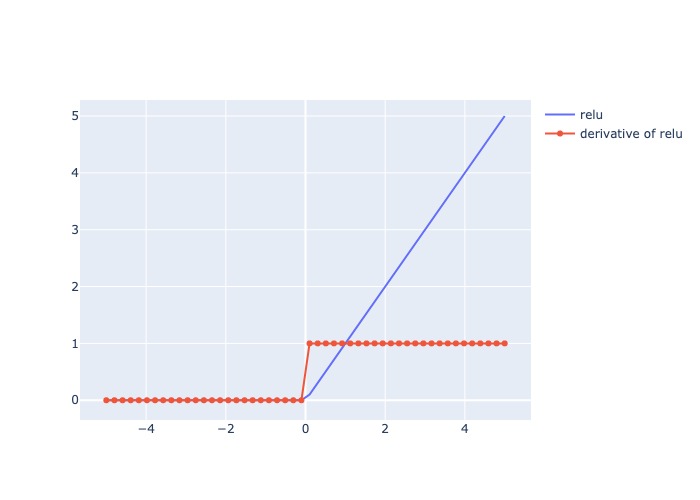
1.2.2.6. ReLU#

\[f(x) = \max(0, x)\]

Mô tả:
- Trả ra input nếu dương, trả ra 0 nếu âm (tạo thành dead node)
Đạo hàm: = 1 cho các giá trị input dương, và = 0 cho các giá trị input âm
Pros:
- Tính toán nhanh
- Có tính chất non-linear
- Đạo hàm không đổi tại các value của x nên khắc phục các giá trị input bất tường hoặc lớn
- best activation function cho CNNs bởi vì hiệu quả cho việc extracting features hoặc for pattern recognition.
- Có thể hoạt động như 1 dropout layer ví dụ như deactive node nếu input = 0
Cons:
- Với x giá trị âm, gradient = 0, có khả năng kết thúc sớm khi học.
- Không khả vi tại 0 nên các continuous output không phù hợp áp dụng
Usage:
- Thường áp dụng cho bài toán CNN, Natural Language Processing, Pattern Recognition
- Trong bài toán nhận diện hình ảnh:
  - Chạy qua các điểm highlight sẽ có update > 0
  - Chạy qua vùng background sẽ không có update

relu = lambda i: max(0,i)

plot_output_and_deriv(af.relu, 'relu')

../../../_images/875763dfb58d80776a2c322d12823b236f5ba897b870a800c38ca3765916a9ee.jpg

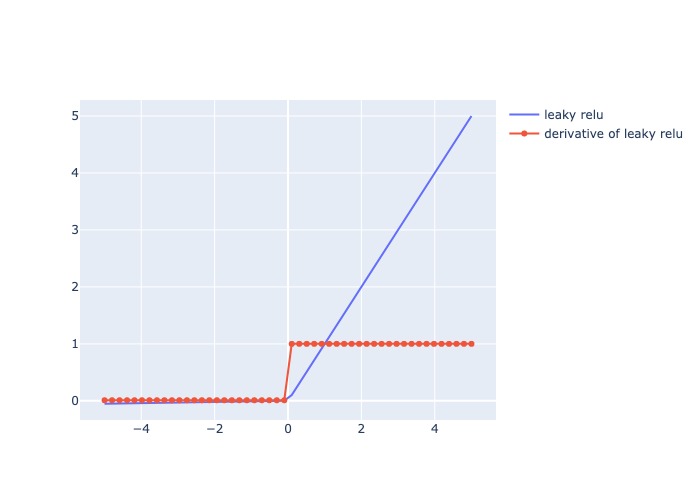
1.2.2.7. Leaky ReLU#

\[\begin{split} LReLU(x)=\left\{{\begin{array}{c l c r}{\alpha x}&{x\leq0}\\ {x}&{x>0}\end{array}}\right. \end{split}\]

where $\alpha$ is a small constant typically set to 0.01.

Mô tả:
- Trả ra x nếu x dương, trả ra số 0.01x nếu x âm (vẫn tạo ra derivative khi x âm)
Đạo hàm: = 1 cho các giá trị input dương, và = 0.01 cho các giá trị input âm
Pros:
- Có ưu điểm của RelU
- Khắc phục sự chết của ReLU khi x âm, thay vào đó derivative = 0.01, tăng độ chính xác so với ReLU
Cons:
- Với x giá trị âm bất kỳ đều có derivative = 0.01, nên quá trình học diễn ra lâu với bất kể x âm như nào
Usage:
- Thường áp dụng cho bài toán CNN, Natural Language Processing, Pattern Recognition

lrelu = lambda i: i if (i >=0) else 0.01*i
lrelu = lambda x: af.relu(x, alpha = 0.01)
plot_output_and_deriv(lrelu, 'leaky relu')

../../../_images/6c3259d321a3fec14e23ed2d3ecb7608997f9c213169bb9f8a21f0ebd2046757.jpg

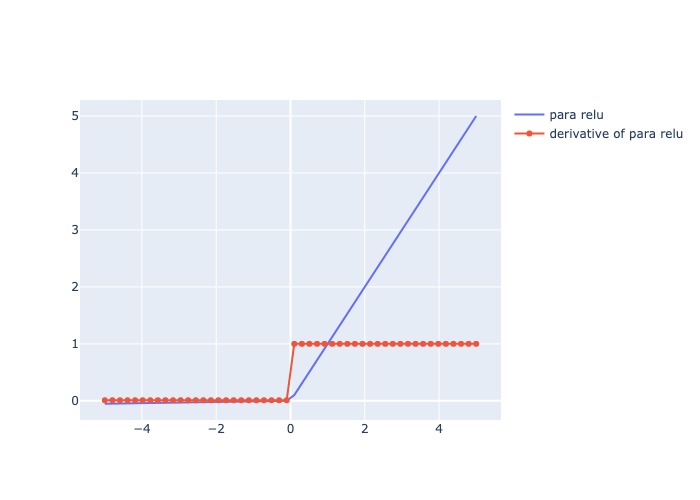
1.2.2.8. Parametric ReLU#

Mô tả:
- Giống Leaky ReLU nhưng $\alpha$ có thể set 1 giá trị bất kỳ
Đạo hàm: = 1 cho các giá trị input dương, và = $\alpha$ cho các giá trị input âm
Pros:
- Tăng độ chính xác và mức độ hội tụ nhanh hơn so với ReLU và Leaky ReLU
Cons:
- Với x giá trị âm bất kỳ đều có derivative = $\alpha$, nên quá trình học diễn ra lâu với bất kể x âm như nào
- Cần check mức độ alpha phù hợp
Usage:
- Thường áp dụng cho bài toán CNN, Natural Language Processing, Pattern Recognition

prelu = lambda x: af.relu(x, alpha = 0.5)
plot_output_and_deriv(lrelu, 'para relu')

../../../_images/47497e15ecf89e598d9f2d1fd3df82725913f41997e6c50975fa91e0987b11f8.jpg

1.2.2.9. Exponential Linear Unit (ELU)#

\[\begin{split} \begin{equation} ELU(x)=\begin{cases} x & \text{if } x>0\\ \alpha(e^x-1) & \text{if } x\leq 0 \end{cases} \end{equation} \end{split}\]

where $\alpha$ is a hyperparameter that controls the slope of the function for negative inputs.

Mô tả:
- Với giá trị input dương x, trả ra hàm linear, còn nếu x âm thì trả ra giá trị gần với mức $-\alpha$, output range (-α,∞)
Đạo hàm: = 1 cho các giá trị input dương, và cho các giá trị input âm
Pros:
- Tăng độ chính xác và mức độ hội tụ nhanh hơn so với ReLU và biến thể
Cons:
- Cần tunning giá trị alpha
- Chi phí tính toán lớn
Usage:
- Thường áp dụng cho bài toán CNN, Natural Language Processing, Pattern Recognition

def ELU(z,α) :
    return z if (z>0) else  (α * (np.exp(z) - 1))

plot_output_and_deriv(af.elu, 'elu')

../../../_images/18938297edb605e1d9cdcb0e66c8a05542ad9e72f118ee1c1d4094d13287072a.jpg

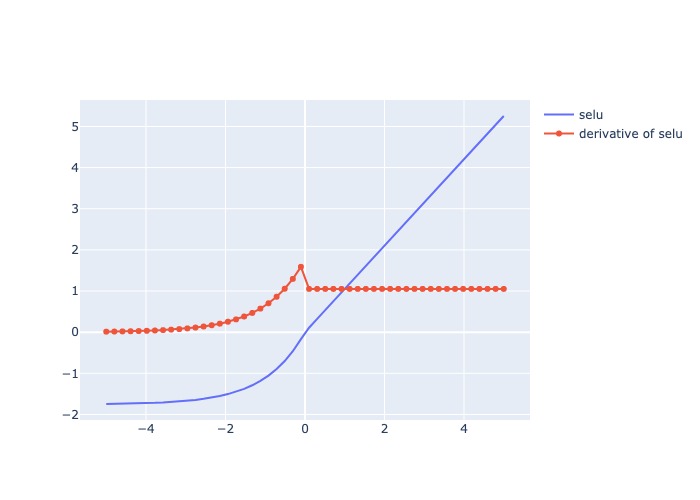
1.2.2.10. Scaled Exponential Linear Unit (SELU)#

\[\begin{split} \text{SELU}(x) = \lambda \begin{cases} x & \text{if } x > 0 \\ \alpha \cdot (\exp(x) - 1) & \text{if } x \leq 0 \end{cases} \end{split}\]

Mô tả:
Đạo hàm: = 1 cho các giá trị input dương, và cho các giá trị input âm
Pros:
- Không có hiện tượng biến mất gradient trong quá trình lan truyền ngược
- Mạng nơ ron hội tụ nhanh hơn.
- Đây là một hàm kích hoạt tự chuẩn hóa, nghĩa là giá trị trung bình trở thành 0 và phương sai thành 1.
- Nó có thể được sử dụng trong các mạng thần kinh rất phức tạp.
Cons:
- Chi phí tính toán lớn
Usage:
- multi-class classification

plot_output_and_deriv(af.selu, 'selu')

../../../_images/13261b7c20732b1aa8f4cabc7c5b00047a3a562a9a6a10f5711653af462caa3e.jpg

1.2.2.11. Swish#

\[\mathrm{Swish}(x) = x \cdot \mathrm{sigmoid}(\beta x) = \]

Mô tả:
- Hàm trả output range (1/e,∞)
- Với input dương, the output là 1 hàm linear của input. Với input âm, cho phép cập nhật 1 phần giá trị tại gần 0, với x quá âm thì ko cập nhật
- Tuỳ thuộc vào $\beta$:
  - $\beta$ = 0: trở thành hàm linear
  - $\beta$ = 1: trở thành hàm linear sigmoid
  - $\beta$ = ∞: trở thành hàm ReLU
Đạo hàm: = 1 cho các giá trị input dương, và cho các giá trị input âm
Pros:
- Tăng độ chính xác hơn ReLU
- Có tính chất non-monotonic cho negative input
- Là hàm liên tục và khả vi mọi điểm
Cons:
- Chi phí tính toán lớn
Usage:
- the same applications as ReLU

plot_output_and_deriv(af.swish, 'swish')

../../../_images/182691bc6842c751395eb3077cc46d725a386a4293dc9219ff3b0f9cf200dcf9.jpg

1.2.3. Loss Function#

Loss thể hiện sự khác biệt / error giữa predictive (với regression là giá trị dự đoán, classification là xác suất) và real value

1.2.3.1. Cross Entropy Loss#

\[ H(p,q) = -\sum_{x} p(x) \log q(x) \]

Trong đó:

x là 1 class trong tập class C
p(x) là xác suất thực của class x
q(x) là xác suất dự đoán của class x

Nếu p(x) == q(x) thì CE = 0, ngược lại nếu p(x) khác xa q(x) thì CE loss sẽ rất lớn

Một số biến thể:
- Categorical Cross Entropy
- Binary Cross Entropy

1.2.3.2. Focal loss#

\[ L_{FL}(p_x) = -\alpha_x(1-p_x)^\gamma \log(p_x) \]

Trong đó:

x là 1 class trong tập class C
$p_x$ là xác suất dự đoán của class x
$\alpha_x$ là the balancing parameter for the true class, nếu $\alpha_x$ gần 1 thì more loss cho y = 1 tức focal_loss(FN) > focal_loss(FP)
$\gamma$ thể hiện mức độ chênh lệch giữa từng class
- $\gamma = 0$: thì FL = Binary CE
- $\gamma$ >> 0: thì càng tăng loss cho class có balance thấp

So sánh với Cross Entropy, Focal tác động thêm trọng số với mục tiêu tăng tỷ trọng class có tỷ lệ thấp và giảm tỷ trọng class có tỷ lệ cao. Ứng dụng vào các bài toán object classification hoặc bài toán có class bị imbalance, khi đó với focal loss sẽ tập trung học những class khó dự đoán, ít update weight bởi các class dễ dự đoán

1.2.4. Points#

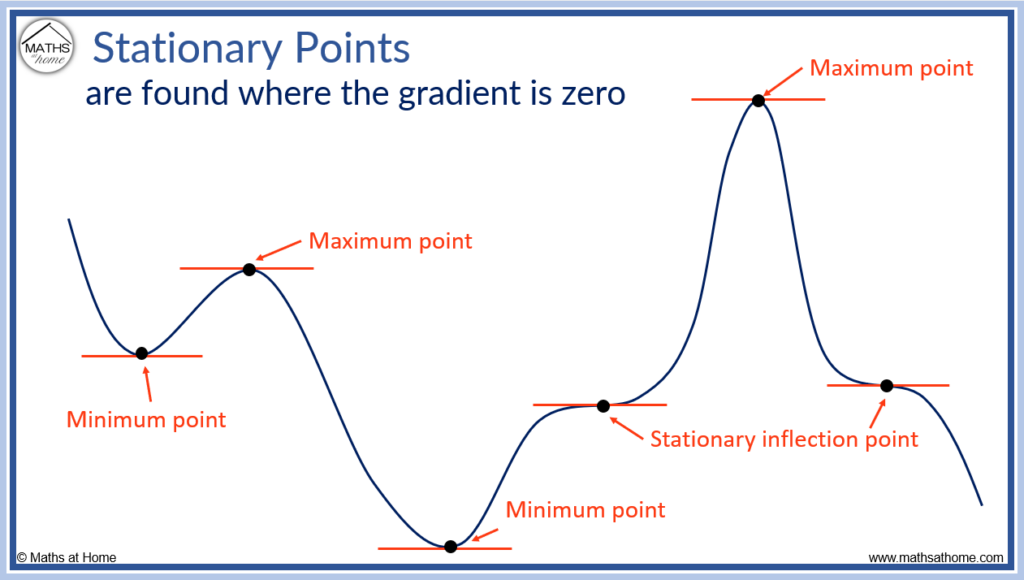
1.2.4.1. Stationary point#

Stationary point t là điểm có đạo hàm f’(x=t) = 0, khi đó điểm t có thể là local minimum/maximum hoặc inflection point.
Inflection point là điểm chuyển tiếp giữa concave up và concave down

1.2.4.2. Critical number#

Điểm cực trị là điểm có đạo hàm tại đó bằng 0 hoặc không xác định

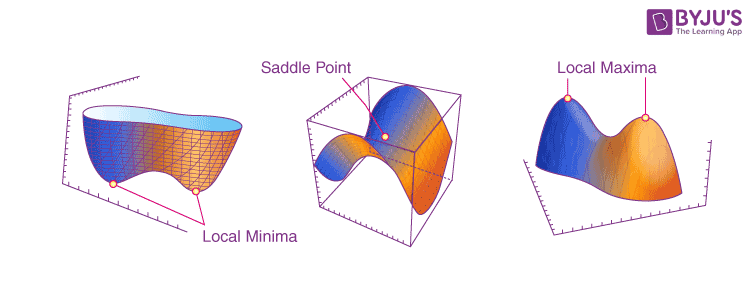
1.2.4.3. Saddle points#

Saddle point là điểm mà tại đó là min point theo 1 chiều x1 nào đó nhưng lại mà max point theo 1 chiều x2 khác (partial derivative = 0 tại các chiều x1, x2)
Trong học máy, máy rất dễ nhầm điểm saddle point là điểm tối ưu

1.2.5. Gradient descent optimization#

1.2.5.1. Gradient descent#

1. Gradient

là 1 vector chứa đạo hàm thành phần của hàm f(x1,x2,..,xn), nhiều gradient tạo thành 1 matrix jacobian

2. Gradient descent

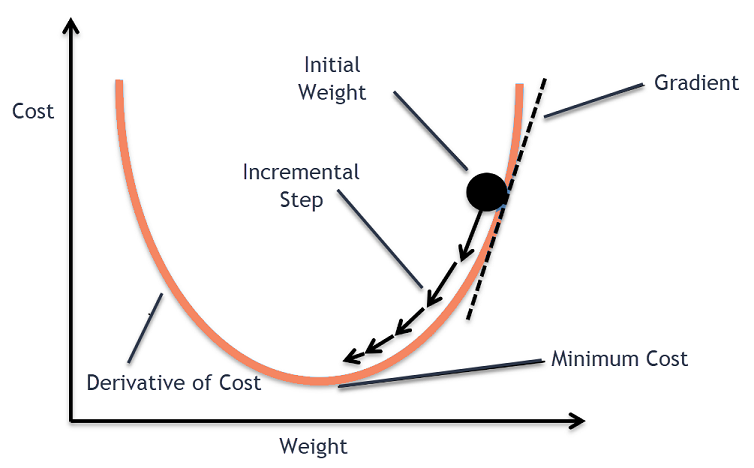
Trong tối ưu, gradient là 1 hyperplane tiếp tuyến của f(x) tại điểm x = t, tương ứng với $W_t$, khi đó hệ số được update theo công thức: $$W_{t+1} = W_t - lr * gradient$$

Thuật toán sẽ stop khi $|W_{t+1} - W_t| <= \epsilon $
gradient = $\frac{\partial L}{\partial w}$ = với hệ số góc của hyperplane = đạo hàm bậc 1 của f(x) tại x=t
Learning rate (lr) sẽ tác động tới khả năng học nhanh/chậm bằng việc điều chỉnh gradient
- Nếu nhiều data có thể set lr nhỏ, và ngược lại
- Có thể để lr = constant hoặc lr giảm dần theo quá trình train ($\frac{lr}{\sqrt{t+1}}$)

1.2.5.2. Các loại gradient descent (GD)#

Các loại GD theo số lượng obs cho mỗi epoch train

1. Vanilla GD/ Batch GD

Update 1 lần trên toàn bộ dataset
Pros : đảm bảo hội tụ được tới GLOBAL minimum cho convex loss hoặc non-convex loss
Cons :
- thuật toán chạy sẽ chậm với dữ liệu lớn,
- ko đủ memory để load hết dữ liệu
- không có khả năng update real-time

2. Stochastic gradient descent (SGD)

Update weight theo từng quan sát lần lượt trên dataset
Pros :
- Không gặp vấn đề về khả năng load, tính toán nhanh
- Có tính train real-time, học online
Cons :
- Do học theo từng obs nên có variance cao
- hướng di chuyển của hàm Loss không ổn định
- Khả năng hội tụ lâu do học không ổn định hoặc đi sai hướng để tìm điểm loss tối ưu

2. Mini-batch gradient descent

Chia data thành nhiều mini batch gồm n obs và lần lượt học theo từng mini-batch. Dữ liệu được lấy random cho từng batch.
Pros :
- Giảm variance của parameter update, more stable convergence
- Có thể sử dụng các thuật toán tối ưu hoá matrix theo từng batch để tăng tính hiệu quả. Ví dụ như batch normalization
Cons :
- Lựa chọn lr: Nếu quá nhỏ sẽ học chậm, nếu quá lớn thì loss sẽ giao động quanh điểm hội tụ hoặc thậm trí đi qua điểm tối ưu
- Chưa giải quyết được vấn đề saddle point

1.2.5.3. Các phương pháp optimize GD#

1.2.5.3.1. Newton#

Là phương pháp tìm nghiệm điểm tối ưu (thay vì GD) bằng hessian matrix và inverse matrix

Không có tính ứng dụng trong thực tiễn cho dữ liệu nhiều chiều hoặc do sự phúc tạp trong tính toán

1.2.5.3.2. Learning rate changes#

1. Decay lr

Learning rate giảm qua mỗi epoch, tuy nhiên ko control được yếu tố còn lại là gradient $$lr_{new} = \frac{lr_{old}}{1 + \text{decay rate} * \text{num rate}}$$

2. Scheduled drop lr

Lr drop sau 1 chu kỳ nhất định

3. Adaptive lr

Lr thay đổi dựa vào value của hàm Loss

4. Cycling lr

Lr thay đổi trong 1 cycle và lặp lại sự thay đổi đó trong cycle tiếp theo.

1.2.5.3.3. Momentum#

Điều chỉnh gradient bằng hướng di chuyển trước đó (bổ sung momentum vào update weight). Quy trình:

Set vận tốc ban đầu $v_0$ = 0
Với mỗi 1 epoch thứ t:

gradient : $\nabla w_{t-1}$
Vận tốc mới: $v_{t}=\gamma v_{t-1} + \eta \nabla w_{t-1}$
Update weight: $W_t = W_{t-1} - v_t$

Lựa chọn $\gamma$:

Nếu $\gamma$ càng lớn thì update càng có hướng smooth do tỷ trọng hướng di chuyển trước đó càng cao, đồng nghĩa với tỷ trọng việc học mới càng thấp.
Nên lựa chọn $\gamma$ in [0.8, 0.99]
$\gamma$ cang cao thì càng làm giảm khả năng hội tụ và có thể vượt qua local minimum hiện tại.

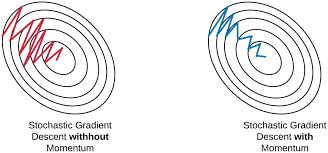
Momentum giúp giảm giao động, nhanh đưa loss về điểm local minimum. Mặt khác, sử dụng vận tốc để update weight nên việc học sẽ không dừng lại ngay cả khi có gradient = 0. Từ đó có khả năng vượt qua local minimum để khám phá các điểm loss mới.

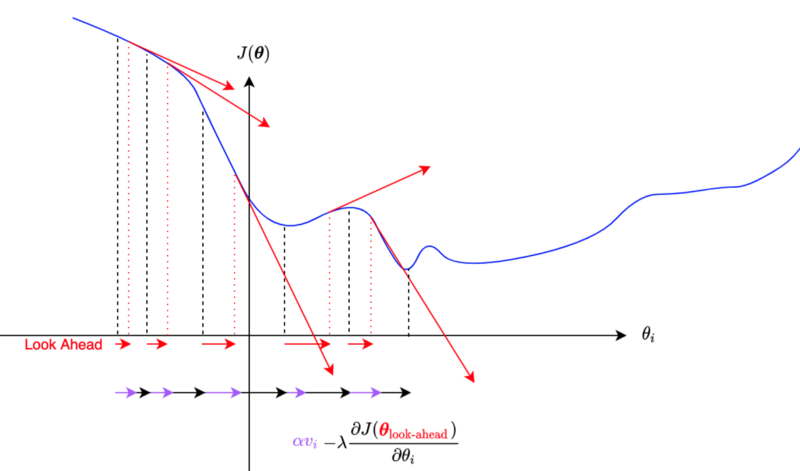
Sử dụng momentum có 1 nhược điểm là khi gần tới điểm hội tụ thì mất nhiều thời gian để dưng lại vì lúc nào cũng có đà di chuyển trước đó

1.2.5.3.4. Nestorov accelerated gradient (NAG)#

NAG giải quyết vấn đề lâu hội tụ tại gần điểm optimize do vấn đề momentum gây ra, bằng việc sử dụng gradient của bước tiếp theo mà ko tính momentum (thay vì gradient của bước hiện tại như momentum)

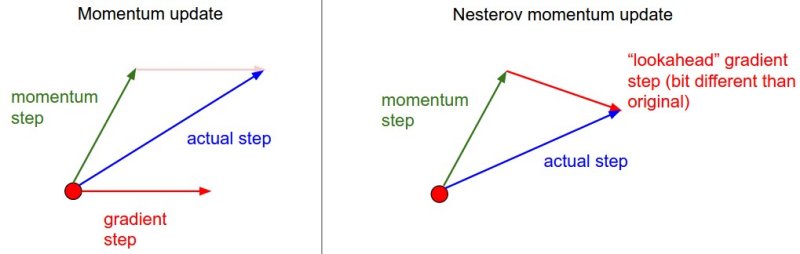
Khi GD ko sử dụng momentum thì “gradient tại điểm xấp xỉ tiếp theo” chính là lượng thay đổi tại điểm mới nhưng ko có momentum

Vận tốc mới: $v_{t}=\gamma v_{t-1} + \eta \nabla (w_{t-1} - \gamma v_{t-1})$
Update weight: $W_t = W_{t-1} - v_t$

1.2.5.3.5. Adagrad#

Điều chỉnh lr bưởi tổng gradient^2 trước đó, do tổng gradient^2 càng ngày càng tăng nên Lr sẽ càng giảm theo thời gian, dẫn tới tác động của gradient hiện tại càng ít, có thể bị mất gradient

1.2.5.3.6. RMSprop#

RMSprop thay đổi hệ số của gradient, khắc phục được nhược điểm của AdaGrad là càng học càng chậm
- Trung bình có trọng số của bình phương các gradient trong quá khứ $G_t$ có trọng số $\gamma$: ${\bf G}_{t} = \gamma{\bf G}_{t-1}+({1-\gamma}){\bf g}_{t}^{2}$
- update weight : ${\bf w}_{t} = {\bf w}_{t-1}-\frac{\eta}{\sqrt{{\bf G}_{t}+\epsilon}}g_t$
Thuật toán RMSProp rất giống với Adagrad ở chỗ cả hai đều sử dụng bình phương của gradient để thay đổi tỉ lệ hệ số.
RMSProp có điểm chung với phương pháp động lượng là chúng đều sử dụng trung bình rò rỉ. Tuy nhiên, RMSProp sử dụng kỹ thuật này để điều chỉnh tiền điều kiện theo hệ số.
Trong thực tế, tốc độ học cần được định thời bởi người lập trình.
Hệ số 𝛾 xác định độ dài thông tin quá khứ được sử dụng khi điều chỉnh tỉ lệ theo từng tọa độ.

1.2.5.3.7. Ada-delta#

Adadelta tương tự như RMSprop, tức là điều chỉnh điều chỉnh mức độ cập nhật gradient vào trọng số thông qua ${\bf G}_{t}$ và ${\bf S}_{t}$, không cần thông qua learning_rate. Cụ thể quy trình tính:

Tính trung bình có trọng số của bình phương các gradient trong quá khứ: $${\bf G}_{t} = \gamma{\bf G}_{t-1}+({1-\gamma}){\bf g}_{t}^{2}$$
Update weight: $${\bf w}_{t} = {\bf w}_{t-1}-\sqrt{\frac{{\bf S}_{t-1}+\epsilon}{{\bf G}_{t}+\epsilon}}g_t$$
Tính trung bình có trọng số của các weight trong quá khứ: $${\bf S}_{t} = \gamma{\bf S}_{t-1}+({1-\gamma}) w_t$$

Tóm lại:

Adadelta không sử dụng tham số tốc độ học. Thay vào đó, nó sử dụng tốc độ thay đổi của chính bản thân các tham số để điều chỉnh tốc độ học.
Adadelta cần sử dụng hai biến trạng thái để lưu trữ các mô-men bậc hai của gradient và của lượng thay đổi trong các tham số.
Adadelta sử dụng trung bình rò rỉ để lưu ước lượng động của các giá trị thống kê cần thiết.

1.2.5.3.8. Adam#

Adam kết hợp sự thay đổi momentum dựa theo gradient bậc 1 và bậc 2 :

tính trung bình có trong số momentum và có hiệu chỉnh: $$ \hat{m}_t = \frac{\beta_1 m_{t-1} + (1- \beta_1) g_t}{1-\beta_1^t} $$
tính trung bình có trong số momentum bậc 2 và có hiệu chỉnh: $$ \hat{v}_t = \frac{\beta_2 v_{t-1} + (1- \beta_2) g_t^2}{1-\beta_2^t} $$
update weight t+1: $$w_{t+1} = w_{t} - \frac{\eta}{\sqrt{\hat{v}_t } +\epsilon} \hat{m}_t$$

default: $\beta_1 = 0.9$ , $beta_2 = 0.999$ , $\epsilon = 10^{-8}$

Tóm lại:

Adam kết hợp các kỹ thuật của nhiều thuật toán tối ưu thành một quy tắc cập nhật khá mạnh mẽ.
Dựa trên RMSProp, Adam cũng sử dụng trung bình động trọng số mũ cho gradient ngẫu nhiên theo minibatch.
Adam sử dụng phép hiệu chỉnh độ chệch (bias correction) để điều chỉnh cho trường hợp khởi động chậm khi ước lượng động lượng và mô-men bậc hai.
Đối với gradient có phương sai đáng kể, chúng ta có thể gặp phải những vấn đề liên quan tới hội tụ. Những vấn đề này có thể được khắc phục bằng cách sử dụng các minibatch có kích thước lớn hơn

1.2.5.3.9. NaAdam#

Tương tự như Adam nhưng NaAdam sử dụng NAG momentum thay cho vanilla momentum component (như của Adam). Nhắc lại là NAG giúp hội tụ tại khu vực minimal nhanh hơn so với vanilla momentum:

tính trung bình có trong số momentum và có hiệu chỉnh: $$ \hat{m}_t = \frac{\beta_1 m_{t-1} + (1- \beta_1) g_t}{1-\beta_1^t} $$
tính trung bình có trong số momentum bậc 2 và có hiệu chỉnh: $$ \hat{v}_t = \frac{\beta_2 v_{t-1} + (1- \beta_2) g_t^2}{1-\beta_2^t} $$
update weight t+1: $$w_{t+1} = w_{t} - \frac{\eta}{\sqrt{\hat{v}_t } +\epsilon} (\beta_1 \hat{m}_t + (1- \beta_1) g_t)$$

default: $\beta_1 = 0.9$ , $beta_2 = 0.999$ , $\epsilon = 10^{-8}$

1.2.5.4. Lựa chọn Loss function#

1. Classification

Log Loss/ Cross entropy Loss: có thể bị loss thay đổi lớn khi gặp các extremely value x, dữ liệu cần phải ở trạng thái balance
Focal loss: phù hợp trong TH dữ liệu imbalance
KL Divergence: xác định tính tương đồng của phân phối của predict và actual
Exponential loss: thường sử dụng khi muốn kết hợp nhiều model độc lập đã có hàm loss riêng, tạo thành 1 hàm loss tổng hợp
Hinge loss: tìm đường phân loại (hyperplane) để chia các nhóm ( tính distance từ hyperplane tới các nhóm)

2. Regression

Root mean squared error
Mean absolute error
Huber loss
Log cosh loss
Quantile loss

1.2.5.5. Quy trình optimize GD#

Initialize weights
Read in samples and actual outputs
WHILE (stopping criterion is not satisfied)
1. Compute prediction output and prediction error by working forward through the layers (input -> hidden -> output)
2. Adjust the weights by working backward through the hidden layers (output -> hidden -> input)
ENDWHILE

1.2.5.5.1. Step1: Feedforward để tính Output and Error#

1.2.5.5.1.1. Prediction error#

Dữ liệu được truyền forward qua các hidden layer và các activate function để đến layer tiếp theo. Tại mỗi layer H gồm có 2 component là pre-activation (tổ hợp tuyến tính của weight, output của activation layer trước và bias của layer H) và activation (là các hàm kích hoạt sẽ nhận input là pre-activation)

The prediction error tại output node là sự khác biệt giữa actual và output dự đoán (giả sử hàm loss là MSE) $$ MSE=\frac{\sum_{k} \sum_{i} (y_i- \hat{y}_i)^2}{\mbox{tổng số obs trong batch}} $$ trong đó:
- i là 1 trong các node output
- k là 1 trong các quan sát trong batch
- $\hat{y}$ là giá trị dự đoán
- $y$ là giá trị thực tế
Hàm Cost chính là trung bình các loss (tương ứng với từng obs trong batch), nếu sử dụng SGD thì Cost = Loss do mỗi epoch có 1 quan sát

1.2.5.5.1.2. Ví dụ tính prediction error#

Bước 1: Dữ liệu ban đầu và các weight ban đầu được lấy random

Bảng input và weight

input	weights	weights	weights
	W0A = 0.5	W0B = 0.7	W0Z = 0.5
x1 = 0.4	W1A = 0.6	W1B = 0.9	WAZ = 0.9
x2 = 0.2	W2A = 0.8	W2B = 0.8	WBZ = 0.9
x3 = 0.7	W3A = 0.6	W3B = 0.4

$y_{actual} = 0.8 $

Bước 2: Tính toán tại node A

Pre-activation tại node A $$ \sum_A =W_{0A} + W_{1A} x_{1} + W_{2A} x_{2} + W_{3A} x_{3} \\ = 0.5+0.6 \times 0.4 + 0.8 \times 0.2 + 0.6 \times 0.7 =1.32 $$
Activiation tại node A giả sử dùng logistic activation function

\[ f(\sum_A) = \frac{1}{1 + \exp(–\sum_A)} =\frac{1}{1 + \exp(–1.32)} = 0.7892. \]

The output tại node $A$: $Output_A =0.7892$

Bước 3: Làm tương tự với các node ta được:

node	summation $\sum$	activation $f(\sum)$
A	1.32	0.7892
B	1.5	0.8176
Z	1.946	0.8750

Output tại output node Z: 0.8750

Bước 4: Tính loss SSE on output Node Z

\[\begin{split} \mbox{SSE} (\mbox{Node Z}) = (\mbox{actual value}- \mbox{predicted value})^2 \\ =(0.8-0.875)^2 = 0.005625 \end{split}\]

1.2.5.5.2. Step2: Backpropagation for Optimizing Weights#

Từ graph, ta hình dung đạo hàm của Loss bởi những biến tương ứng được tính thông qua chain rule như thế nào:

$ \begin{equation} \begin{split} \frac{\partial L}{\partial w_2} & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial w_2}\\ & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z_2} \frac{\partial z_2}{\partial w_2} \\ \end{split} \end{equation} $

Làm tương tự với the weight $w_1$:

$ \begin{equation} \begin{split} \frac{\partial L}{\partial w_1} & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial w_1}\\ & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z_2} \frac{\partial z_2}{\partial w_1} \\ & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z_2} \frac{\partial z_2}{\partial h} \frac{\partial h}{\partial w_1} \\ & = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z_2} \frac{\partial z_2}{\partial h} \frac{\partial h}{\partial z_1} \frac{\partial z_1}{\partial w_1} \end{split} \end{equation} $

Các giá trị $\frac{\partial L}{\partial w_1}$ có thể sử dụng lại 1 phần tính toán $\frac{\partial L}{\partial w_2}$.

Với bias ta tính $\frac{\partial L}{\partial b_1}$:

$ \begin{equation} \begin{split} \frac{\partial L}{\partial b_1} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z_2} \frac{\partial z_2}{\partial h} \frac{\partial h}{\partial z_1} \frac{\partial z_1}{\partial b_1} \end{split} \end{equation} $

1.2.5.5.3. Ví dụ#

# dataset
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.special import expit as sigmoid
import copy


np.random.seed(0)

def generate_dataset(N_points):
    # 1 class
    radiuses = np.random.uniform(0, 0.5, size=N_points//2)
    angles = np.random.uniform(0, 2*math.pi, size=N_points//2)
    
    x_1 = np.multiply(radiuses, np.cos(angles)).reshape(N_points//2, 1)
    x_2 = np.multiply(radiuses, np.sin(angles)).reshape(N_points//2, 1)
    X_class_1 = np.concatenate((x_1, x_2), axis=1)
    Y_class_1 = np.full((N_points//2,), 1)
        
    # 0 class
    radiuses = np.random.uniform(0.6, 1, size=N_points//2)
    angles = np.random.uniform(0, 2*math.pi, size=N_points//2)
    
    x_1 = np.multiply(radiuses, np.cos(angles)).reshape(N_points//2, 1)
    x_2 = np.multiply(radiuses, np.sin(angles)).reshape(N_points//2, 1)
    X_class_0 = np.concatenate((x_1, x_2), axis=1)
    Y_class_0 = np.full((N_points//2,), 0)
        
    X = np.concatenate((X_class_1, X_class_0), axis=0)
    Y = np.concatenate((Y_class_1, Y_class_0), axis=0)
    return X, Y
    
N_points = 1000
X, Y = generate_dataset(N_points)
print(X.shape)

plt.scatter(X[:N_points//2, 0], X[:N_points//2, 1], color='red', label='class 1') 
plt.scatter(X[N_points//2:, 0], X[N_points//2:, 1], color='blue', label='class 0')
plt.legend(loc=9, bbox_to_anchor=(0.5, -0.1), ncol=2)
plt.show()

(1000, 2)

../../../_images/5a099dcd44bd6326bdfabbb7e16a481aa9f6c18fc21931326bc3a08cc3da4c52.png

Mô phỏng mạng neural network

Mô phỏng mạng by tensorflow playground

Từ dữ liệu, mỗi quan sát được mô phỏng bởi 2 features $ \begin{equation} \begin{split} \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} \end{split} \end{equation} $. Biến target y có 2 giá trị 0 và 1 nên output layer có 1 node. Ta sử dung 1 hidden layer cấu tạo bởi 3 node.

Tổng hợp lại:

pre-activation: $ \mathbf{z_1} = \mathbf{W_1 x} + \mathbf{b_1} $, với $ \begin{equation} \begin{split} \mathbf{W_1} = \begin{bmatrix} w^{(1)}_{1,1} & w^{(1)}_{2,1} \\ w^{(1)}_{1,2} & w^{(1)}_{2,2} \\ w^{(1)}_{1,3} & w^{(1)}_{2,3} \\ \end{bmatrix} \end{split} \end{equation} $, $ \begin{equation} \begin{split} \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} \end{split} \end{equation} $ và $ \begin{equation} \begin{split} \mathbf{b_1} = \begin{bmatrix} b^{(1)}_{1}\\ b^{(1)}_{2}\\ b^{(1)}_{3}\\ \end{bmatrix} \end{split} \end{equation} $

Hàm activation: $ \mathbf{h} = \sigma(\mathbf{z_1}) $

Tương tự: $ \mathbf{z_2} = \mathbf{W_2 h} + b_2$ with $ \begin{equation} \begin{split} \mathbf{W_2} = \begin{bmatrix} w^{(2)}_{1,1} & w^{(2)}_{2,1} & w^{(2)}_{3,1} \end{bmatrix} \end{split} \end{equation} $, and $b_2 = b^{(2)}_1$.

Output layer: $ \mathbf{y} = \sigma(\mathbf{z_2}) $

Phương trình phía trên giúp dự đoán y từ single data point$ \begin{equation} \begin{split} \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} \end{split} \end{equation} $.

Ta chuyển đổi sang sử dụng matrix data X $\mathbf{X}$ with the shape $(N_{points}, 2)$: $ \begin{equation} \begin{split} \mathbf{X} = \begin{bmatrix} x_1^{(1)} & x_2^{(1)} \\ x_1^{(2)} & x_2^{(2)} \\ . & . \\ . & . \\ . & . \\ x_1^{(N_{points})} & x_2^{(N_{points})} \\ \end{bmatrix} \end{split} \end{equation} $

Trong đó mỗi dòng là 1 data point.

Viết lại các phương trình trên:

$ \mathbf{Z_1} = \mathbf{X W_1^T} + \mathbf{1 b_1^T} $, với $ \begin{equation} \begin{split} \mathbf{1} = \begin{bmatrix} 1 \\ 1 \\ . \\ . \\ . \\ 1 \\ \end{bmatrix} \end{split} \end{equation} $ a vector of shape $(N_{points}, 1)$ whose elements are all 1.

$ \mathbf{H} = \sigma(\mathbf{Z_1}) $

$ \mathbf{Z_2} = \mathbf{H W_2^T} + \mathbf{1} b_2$, with $\mathbf{1}$ is as defined above.

$ \mathbf{Y} = \sigma(\mathbf{Z_2}) $

### Forward propagation
# activation function giả sử là hàm sigmoid

# khởi tại initial parameters
weights = {
    'W1': np.random.randn(3, 2),
    'b1': np.zeros(3),
    'W2': np.random.randn(3),
    'b2': 0,
}

def forward_propagation(X, weights):    
    # this implement the vectorized equations defined above.
    Z1 = np.dot(X, weights['W1'].T)  + weights['b1']
    H = sigmoid(Z1)
    Z2 = np.dot(H, weights['W2'].T) + weights['b2']
    Y = sigmoid(Z2)    
    return Y, Z2, H, Z1

Loss function

Use the cross entropy function cho bài toàn classification:

\[L(y, y_T) = \frac{1}{N_{points}} \sum_{n=1}^{N_{points}}\left( -y_T^{(n)} \log(y^{(n)}) - (1-y_T^{(n)}) \log(1-y^{(n)})\right) \]

trong đó $y^{(n)}$ là output dự đoán của forward propagation $ \begin{equation} \begin{split} \mathbf{x^{(n)}} = \begin{bmatrix} x^{(n)}_1 \\ x^{(n)}_2 \\ \end{bmatrix} \end{split} \end{equation} $, và $y_T^{(n)}$ là label actual.

To understand why the cross entropy is a good choice as a loss function, I highly recommend this video from Aurelien Geron.

def Lo(Y, Y_T, N_points):
    return (1/N_points) * np.sum(-Y_T * np.log(Y) - (1 - Y_T) * np.log(1 - Y))

Backpropagation We have everything we need now to define the back_propagation function. First let’s write again down the gradient equations:

$ \frac{\partial L}{\partial \mathbf{W_2}} = \frac{\partial L}{\partial \mathbf{Y}}\frac{\partial \mathbf{Y}}{\partial \mathbf{Z_2}}\frac{\partial \mathbf{Z_2}}{\partial \mathbf{W_2}}$

$ \frac{\partial L}{\partial \mathbf{b_2}} = \frac{\partial L}{\partial \mathbf{Y}}\frac{\partial \mathbf{Y}}{\partial \mathbf{Z_2}}\frac{\partial \mathbf{Z_2}}{\partial \mathbf{b_2}}$

$ \frac{\partial L}{\partial \mathbf{W_1}} = \frac{\partial L}{\partial \mathbf{Y}}\frac{\partial \mathbf{Y}}{\partial \mathbf{Z_2}}\frac{\partial \mathbf{Z_2}}{\partial \mathbf{H}}\frac{\partial \mathbf{H}}{\partial \mathbf{Z_1}}\frac{\partial \mathbf{Z_1}}{\partial \mathbf{W_1}}$

$ \frac{\partial L}{\partial \mathbf{b_1}} = \frac{\partial L}{\partial \mathbf{Y}}\frac{\partial \mathbf{Y}}{\partial \mathbf{Z_2}}\frac{\partial \mathbf{Z_2}}{\partial \mathbf{H}}\frac{\partial \mathbf{H}}{\partial \mathbf{Z_1}}\frac{\partial \mathbf{Z_1}}{\partial \mathbf{b_1}}$

We therefore need the following partial derivatives, which can be easily obtained:

$ \frac{\partial L}{\partial\mathbf{Y}} = \frac{1}{N} \frac{\mathbf{Y}-\mathbf{Y_T}}{\mathbf{Y}(1-\mathbf{Y})}$

$ \frac{\partial \mathbf{L}}{\partial\mathbf{Z_2}} = \frac{\partial L}{\partial\mathbf{Y}} .\left(\sigma(\mathbf{Z_2})(1-\sigma(\mathbf{Z_2}))\right)$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{W_2}} = \mathbf{H^T} \frac{\partial \mathbf{L}}{\partial\mathbf{Z_2}}$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{b_2}} = \left(\frac{\partial \mathbf{L}}{\partial\mathbf{Z_2}} \right)^T\mathbf{1}$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{H}} = \frac{\partial \mathbf{L}}{\partial\mathbf{Z_2}} \mathbf{W_2^T}$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{Z_1}} = \frac{\partial \mathbf{L}}{\partial \mathbf{H}}.\left(\sigma(\mathbf{Z_1})(1-\sigma(\mathbf{Z_1}))\right)$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{W_1}} = \left(\frac{\partial \mathbf{L}}{\partial \mathbf{Z_1}}\right)^T\mathbf{X}$

$ \frac{\partial \mathbf{L}}{\partial \mathbf{b_1}} = \left(\frac{\partial \mathbf{L}}{\partial \mathbf{Z_1}}\right)^T\mathbf{1}$

We can now define the code for the backpropagation:

def back_propagation(X, Y_T, weights):
    N_points = X.shape[0]
    
    # forward propagation
    Y, Z2, H, Z1 = forward_propagation(X, weights)
    L = Lo(Y, Y_T, N_points)
    
    # back propagation
    dLdY = 1/N_points * np.divide(Y - Y_T, np.multiply(Y, 1-Y))
    dLdZ2 = np.multiply(dLdY, (sigmoid(Z2)*(1-sigmoid(Z2))))
    dLdW2 = np.dot(H.T, dLdZ2)
    dLdb2 = np.dot(dLdZ2.T, np.ones(N_points))
    dLdH = np.dot(dLdZ2.reshape(N_points, 1), weights['W2'].reshape(1, 3))
    dLdZ1 = np.multiply(dLdH, np.multiply(sigmoid(Z1), (1-sigmoid(Z1))))
    dLdW1 = np.dot(dLdZ1.T, X)
    dLdb1 = np.dot(dLdZ1.T, np.ones(N_points))
    
    gradients = {
        'W1': dLdW1,
        'b1': dLdb1,
        'W2': dLdW2,
        'b2': dLdb2,
    }
    return gradients, L

Training: gradient descent

At every iteration the weights and the biases are updated as $ w^{(n+1)} = w^{(n)} - \epsilon \frac{\partial L}{\partial w} $

def training(initial_weights, epochs = 2000, epsilon = 1, plot_loss = True):
    weights = copy.deepcopy(initial_weights)
    losses = []
    for epoch in range(epochs):
        gradients, L = back_propagation(X, Y, weights)
        for weight_name in weights:
            weights[weight_name] -= epsilon * gradients[weight_name]
        losses.append(L)
        if (epoch % 100) == 0 :
            print("epoch {} with loss: {}".format(epoch, L), end = "\r")
            
    if plot_loss:
        plt.scatter(range(epochs), losses)
        plt.title('Training Loss')
        plt.xlabel('Epoch')
        plt.ylabel('Loss')
        plt.show()
        
    return losses, weights
    
losses, learning_weights = training(weights, epochs = 2000, epsilon = 1, plot_loss = True)

epoch 1900 with loss: 0.06257494502066781

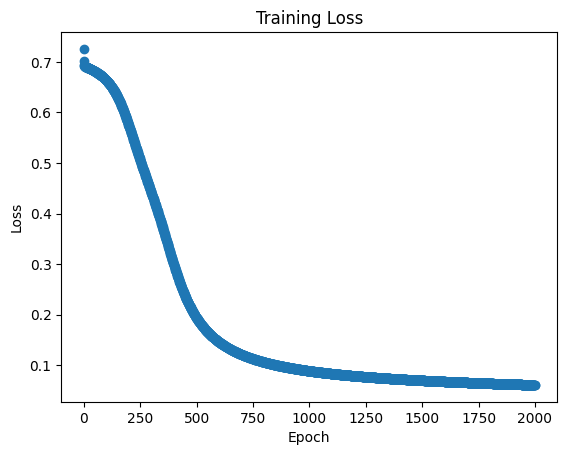
../../../_images/e63e29c3e13b695659f2ec2341f0447900b3854329bb798b14a22e81d8daa0f5.png

Visualize what the network learned

def visualization(X_data, weights, title = None, superposed_training=False):
    N_test_points = X_data.shape[0]
    xs = np.linspace(1.1*np.min(X_data), 1.1*np.max(X_data), N_test_points)
    datapoints = np.transpose([np.tile(xs, len(xs)), np.repeat(xs, len(xs))])
    Y_initial = forward_propagation(datapoints, weights)[0].reshape(N_test_points, N_test_points)
    X1, X2 = np.meshgrid(xs, xs)
    plt.pcolormesh(X1, X2, Y_initial)
    plt.colorbar(label='P(1)')
    if superposed_training:
        plt.scatter(X_data[:N_points//2, 0], X_data[:N_points//2, 1], color='red') 
        plt.scatter(X_data[N_points//2:, 0], X_data[N_points//2:, 1], color='blue') 
    plt.title(title)
    plt.show()
    
visualization( X, weights,  'Before learning')
visualization( X, learning_weights, 'After learning', superposed_training=True)

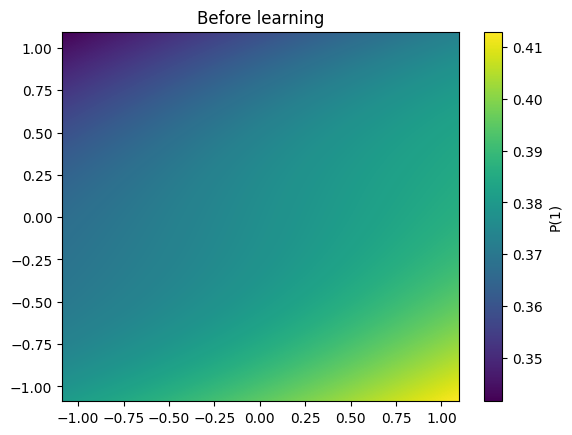
../../../_images/cc2f89bf0ccdab3de9c1216b4afe7972d7267d5967e8db6a38c2093bb68cf3a0.png

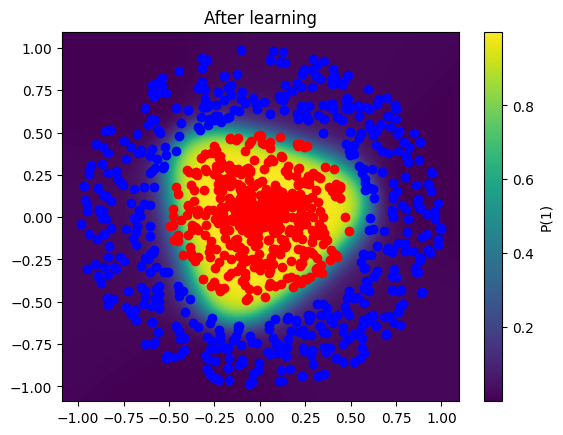
../../../_images/16003a7b1597d95574b8d4af03275a5637146a7dba8f14bbb82b8295cb3e6b36.png

1.2.6. Regularization in NN#

1.2.6.1. L1/L2 regularization#

L1 regularization

Hàm Cost/Loss sẽ được bổ sung penalty L1 tương ứng theo khoảng cách manhattan
Khi đó hàm Loss sẽ luôn tiến sát về 0 nhưng cách 1 khoảng tối thiểu là mức penalty
- Chỉ có giới hạn số điểm để Loss chạm được L1 min (điểm mà error = 0)

L2 regularization

Hàm Cost/Loss sẽ được bổ sung penalty L2 tương ứng theo khoảng cách euclidean
Khi đó hàm Loss sẽ luôn tiến sát về 0 nhưng cách 1 khoảng tối thiểu là mức penalty euclidean,
Có nhiều nghiệm thoả mãn min L2 hơn so với L1

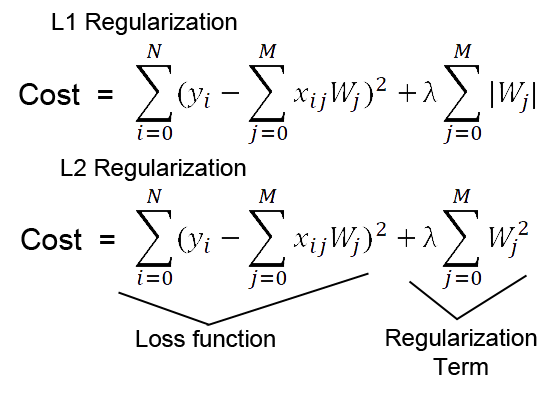
Nếu máy học W lớn thì Loss giảm nhưng Regularization tăng
Một hàm Cost tốt khi cả loss và Regu đều giảm
Sử dụng L2 phạt nặng hơn L1 khi W tăng mạnh

1.2.6.2. Early stopping#

1. Giới hạn vòng lặp : MLPClassifier(max_iter=300)

nhược điểm là model có thể dừng trước khi hội tụ

2. So sánh gradient

So sánh gradient của nghiệm 2 lần update liên tiếp nếu chênh lệch với giá trị threshold
ảnh hưởng performance nếu việc tính toán đạo hàm quá phức tạp khi có dữ liệu lớn, ko được hưởng lợi từ SGD hoặc mini-batch GD

3. So sánh Loss: MLPClassifier(tol=0.0001)

So sánh los của 1 vài lần update, nếu hàm loss it thay đổi thì dừng

3. Đặt ngưỡng dừng cho Loss:

Thiết lập ngưỡng chấp nhận được cho Loss, nếu loss trong tập validate dưới mức đó trong quá trình training thì dừng lại

1.2.6.3. Dropout regularization#

Việc quá nhiều nút (full connected) dẫn tới các nút phụ thuộc nhiều vào nhau. Vậy nên cần tắt bớt 1 số nút trong mạng thông qua việc set mỗi node có xác suất activate là p và deactivate là 1-p

Tuy nhiên có thể làm mất thông tin trong quá trình học do tắt 1 số nút quan trọng

1.2.6.4. Training knowledge augmentation#

Tạo thêm obs xung quanh các raw obs

1.2.6.5. Batch Normalization#

BN đề cập đến việc chuẩn hóa giá trị input của layer bất kỳ. Chuẩn hóa có nghĩa là đưa phân phối của layer về xấp xỉ phân phối chuẩn với trung bình xấp xỉ 0 và phương sai xấp xỉ 1. Về mặc toán học, Batch Normalization (BN) thực hiện như sau: với mỗi layer, BN tính giá trị trung bình và phương sai của nó. Sau đó sẽ lấy giá trị đặc trưng trừ giá trị trung bình , sau đó chia cho độ lệch chuẩn. Data được chia nhỏ thành nhiều batch và normalize từng batch giúp:

Giảm tác động khi thay đổi nhỏ của weight
Dễ dàng optimize
Các weight có cùng cơ sở để so sánh với nhau
Giảm sự biến thiên giữa các batch

Normalize input $$\hat{x}_{i}\frac{x_{i}-\mu_{B}}{\sqrt{\sigma_{B}^{2}+\epsilon}}$$

Tác dụng của normalized

Speedup training time
Hạn chế vanishing gradient (bị mất gradient theo lan truyền ngược)
Giảm overfitting do giảm tác động của noise và cố định phân phối của các feature qua các lớp layer. Sử dụng batch normalization, chúng ta sẽ không cần phải sử dụng quá nhiều dropput và điều này rất có ý nghĩa vì chúng ta sẽ không cần phải lo lắng vì bị mất quá nhiều thông tin khi dropout weigths của mạng

Hạn chế của BN

BN thực hiện lại các phép tính trình bày phía trên qua các lần lặp, cho nên, về lý thuyết, chúng ta cần batch size đủ lớn để phân phối của mini-batch xấp xỉ phân phối của dữ liệu. Điều này gây khó khăn cho các mô hình đòi hỏi ảnh đầu vào có chất lượng cao (1920x1080) như object detection, semantic segmentation, … Việc huấn luyện với batch size lớn làm mô hình phải tính toán nhiều và chậm
Với Batch size = 1, giá trị phương sai sẽ là 0. Do đó BN sẽ không hoạt động hiệu quả
BN không hoạt động tốt với RNN. Lý do là RNN có các kết nối lặp lại với các timestamps trước đó, và yêu cầu các giá trị beta và gamma khác nhau cho mỗi timestep, dẫn đến độ phức tạp tăng lên gấp nhiều lần, và gây khó khăn cho việc sử dụng BN trong RNN.
Trong quá trình test, BN không tính toán lại giá trị trung bình và phương sai của tập test. Mà sử dụng giá trị trung bình và phương sai được tính toán từ tập train. Điều này làm cho việc tính toán tăng thêm. Ỏ pytorch, hàm model.eval() giúp chúng ta thiết lập mô hình ở chế độ evaluation. Ở chế độ này, BN layer sẽ sử dụng các giá trị trung bình và phương sai được tính toán từ trước trong dữ liệu huấn luyện. Giúp cho chúng ta không phải tính đi tính lại giá trị này.