1.1. Linear algebra#
import numpy as np
import scipy
import pandas as pd
1.1.1. Matrix and vector#
1.1.1.1. Vector#
Vector thể hiện một quan sát gồm có các feature
v = np.array([1,2,3,2])
v
array([1, 2, 3, 2])
# Create an array of evenly
v2 = np.arange(10,25,5)
v2
array([10, 15, 20])
# Create an array of evenly - array tuyen tinh
np.linspace(0,10,6)
array([ 0., 2., 4., 6., 8., 10.])
# 2 vector
C = np.array([2,40])
D = np.array([5,-7])
C@D
-270
1.1.1.1.1. tích vô hướng 2 vector#
A = np.array([0,2])
B = np.array([3,0])
np.inner(A, B)
0
1.1.1.2. Create matrix#
Matrix thể hiện tập hợp nhiều vector
1.1.1.2.1. custom matrix#
# Taking a 3 * 3 matrix
A = np.array([[1, 2, 3],
[0, -2, -2],
[2, 0, 4]])
A.shape
(3, 3)
# Taking a 2 * 2 * 3 matrix (3 dimensions)
ar_3d = np.array([[(1.5,2,3), (4,5,6)], [(3,2,1), (4,5,6)]], dtype = float)
ar_3d.shape
(2, 2, 3)
1.1.1.2.2. array of zeros#
# Create an array of zeros
np.zeros((3,4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
1.1.1.2.3. array of ones#
# Create an array of ones
np.ones((2,3,4))
array([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
1.1.1.2.4. array of constant#
# Create a constant array
np.full((2,2),7)
array([[7, 7],
[7, 7]])
1.1.1.2.5. matrix don vi#
# Create a 2X2 identity matrix - matrix don vi
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
1.1.1.2.6. random matrix#
# Create an array with random values
np.random.random((2,2))
array([[0.6686836 , 0.22002484],
[0.91715112, 0.93238177]])
# Create an empty array
np.empty((3,4))
array([[1.5, 2. , 3. , 4. ],
[5. , 6. , 3. , 2. ],
[1. , 4. , 5. , 6. ]])
1.1.1.3. Matrix function#
1.1.1.3.1. get info#
# Array dimensions - xem chieu array
c.shape
(2, 2, 3)
# Length of array - so phan tu array ben ngoai
len(c)
2
# Number of array dimensions - so chieu
c.ndim
3
# Number of array elements - so elements trong ca array
c.size
12
# Data type of array elements
b.dtype
dtype('float64')
# Name of data type
b.dtype.name
'float64'
# Convert an array to a different type
b.astype(int)
array([[1, 2, 3],
[4, 5, 6]])
1.1.1.3.2. resize , reshape#
# Flatten the array
A.ravel()
array([ 1, 2, 3, 0, -2, -2, 2, 0, 4])
# reshape
A.reshape(9,1)
array([[ 1],
[ 2],
[ 3],
[ 0],
[-2],
[-2],
[ 2],
[ 0],
[ 4]])
# resize
A.resize((3,6),refcheck=False)
A
array([[ 1, 2, 3, 0, -2, -2],
[ 2, 0, 4, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0]])
1.1.1.3.3. concat#
# append
A = np.array([[1, 2, 3]])
np.append(A,A)
array([1, 2, 3, 1, 2, 3])
# Combining:
A = np.array([[1, 2, 3],[4, 5, 6]])
B = np.array([[11, 12, 13],[14, 15, 16]])
# concatenate row-wise
C = np.concatenate((A,B),axis=0)
print(C)
[[ 1 2 3]
[ 4 5 6]
[11 12 13]
[14 15 16]]
# concatenate column-wise
np.concatenate((A,B),axis=1)
array([[ 1, 2, 3, 11, 12, 13],
[ 4, 5, 6, 14, 15, 16]])
# stack
A = np.array([[1, 2, 3],[4, 5, 6]])
np.hstack((A,B))
array([[ 1, 2, 3, 11, 12, 13],
[ 4, 5, 6, 14, 15, 16]])
1.1.1.3.4. split#
# Splitting:
# - Splits array into 3 sub-arrays
np.split(A,2, axis = 0)
[array([[1, 2, 3]]), array([[4, 5, 6]])]
np.split(A,3, axis = 1)
[array([[1],
[4]]),
array([[2],
[5]]),
array([[3],
[6]])]
1.1.1.3.5. filter matrix#
# boolean array
A < 5
array([[ True, True, True],
[ True, False, False]])
A[A < 5]
array([1, 2, 3, 4])
np.where(A < 5, A, B)
array([[ 1, 2, 3],
[ 4, 15, 16]])
1.1.1.3.6. expand matrix#
# pad
print(A)
# pad axis 0 with 1 before and 3 after, axis 2 with 2 before and 4 after
np.pad(A, ((1,3), (2,4)))
[[1 2 3]
[4 5 6]]
array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 2, 3, 0, 0, 0, 0],
[0, 0, 4, 5, 6, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0]])
# pad axis 0 with 1 before and 3 after, axis 2 with 2 before and 4 after
np.pad(A.astype(float), ((1,3), (2,4)), mode = 'constant', constant_values = np.nan)
array([[nan, nan, nan, nan, nan, nan, nan, nan, nan],
[nan, nan, 1., 2., 3., nan, nan, nan, nan],
[nan, nan, 4., 5., 6., nan, nan, nan, nan],
[nan, nan, nan, nan, nan, nan, nan, nan, nan],
[nan, nan, nan, nan, nan, nan, nan, nan, nan],
[nan, nan, nan, nan, nan, nan, nan, nan, nan]])
A = np.array([[1, np.nan, 30],[-4, 5, -60]])
np.pad(A.astype(float), ((1,3), (2,4)), mode = 'edge')
array([[ 1., 1., 1., nan, 30., 30., 30., 30., 30.],
[ 1., 1., 1., nan, 30., 30., 30., 30., 30.],
[ -4., -4., -4., 5., -60., -60., -60., -60., -60.],
[ -4., -4., -4., 5., -60., -60., -60., -60., -60.],
[ -4., -4., -4., 5., -60., -60., -60., -60., -60.],
[ -4., -4., -4., 5., -60., -60., -60., -60., -60.]])
1.1.1.4. Math matrix function#
1.1.1.4.1. transpose#
# transpose
A = np.array([[1, 2, 3],[4, 5, 6]])
A.T
array([[1, 4],
[2, 5],
[3, 6]])
1.1.1.4.2. nhân matrix#
# mũ matrix lên cơ số n
np.power(A,2)
array([[ 1, 4, 9],
[16, 25, 36]])
# mũ matrix lên cơ số n
A = np.array([[1, 2, 3],[4, 5, 6],[4, 5, 6]])
B = np.array([[5, 3, 3],[2, 2, 2],[4, 5, 6]])
np.power(B,A)
array([[ 5, 9, 27],
[ 16, 32, 64],
[ 256, 3125, 46656]])
# multiple matrix - thuc hien nhan cac phan tu ở vị trí giống nhau
A = np.array([[1, 2, 3],[4, 5, 6]])
A * A
array([[ 1, 4, 9],
[16, 25, 36]])
A = np.array([[1, 2, 3],[4, 5, 6]])
B = np.array([[11, 12,13]])
A * B
array([[11, 24, 39],
[44, 60, 78]])
# Nhan matrix - This will return dot product 2x3 * 3x1 = 2x1
res = np.dot(A,B.T)
res
array([[ 74],
[182]])
# or
A@B.T
array([[ 74],
[182]])
# 2 vector
C = np.array([2,40])
D = np.array([5,-7])
C@D
-270
# tinh cos goc 2 vector c, d
norm_c = np.linalg.norm(C)
norm_d = np.linalg.norm(D)
cos_cd = C@D / (norm_c * norm_d)
# tinh goc
radians_cd = np.arccos(cos_cd)
degree_cd = np.degrees(radians_cd)
# độ lớn
magnitude_cd = norm_c * norm_d
print(cos_cd)
print(degree_cd)
print(magnitude_cd)
-0.7836925573198097
141.59991698191385
344.52285845789686
# giai he phuong trinh
# 3a + 4b + 10c = 410
# 6a + 6b + 1c = 210
# 2a + 7b + 15c = 610
X = np.array([
[3,4,10],
[6,6,1],
[2,7,15],
])
Y = np.array([
[410],
[210],
[610],
])
X_inv = np.linalg.inv(X)
nghiem = X_inv@Y
a,b,c = (nghiem.T[0].round())
print(a,b,c)
10.0 20.0 30.0
# check 2 matrix co giong nhau hay k ?
np.allclose(np.eye(X.shape[0]),X@X_inv)
True
1.1.1.5. inverse matrix#
A = np.array([[2,-1],[1,1]])
B = np.linalg.inv(A)
print(B)
[[ 0.33333333 0.33333333]
[-0.33333333 0.66666667]]
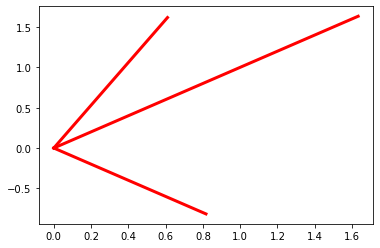
1.1.1.6. Eigenvalue - Eigenvector#
Khi ma trận hiệp phương sai A (thể hiện biến thiên của các biến với nhau) khi chiếu lên chiều mới là u (tức A𝛍) thì kết quả thu được chỉ là tỷ lệ của chiều đó (𝛌𝛍), tức các biến thiên ban đầu có ựu độc lập với nhau theo chiều u và có tỷ lệ độ dài trên chiều u –> thể hiện đầy đủ covariance A. Khi đó: 𝛌 eigen value, 𝛍 eigen vector của A
import matplotlib.pyplot as plt
arr = np.array([[1,-3,3],[3,-5,3],[6,-6,4]])
e,v = np.linalg.eig(arr)
for ie, iv in zip(e, v.T): # v.T do vector theo cột, cần T để lấy ra value (CHÚ Ý - VECTOR ở dạng cột)
plt.plot([0,ie * iv[0]], [0, ie * iv[1]], color = 'r', lw = 3)
plt.show()
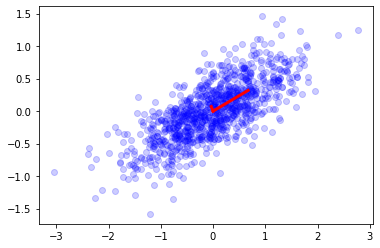
CenterPoint = np.array([0,0])
CovXY_random = np.array([[0.6, 0.25],[0.25,0.2]])
n = 1000
Points = np.random.multivariate_normal(CenterPoint, CovXY_random, n).T
cov = np.cov(Points)
plt.scatter(Points[0,:], Points[1,:], color = 'b', alpha = 0.2)
# tim eigenvalue, eigenvector
# ie là value của vector, iv là chiều vector
e,v = np.linalg.eig(cov)
for ie, iv in zip(e, v.T): # v.T do vector theo cột, cần T để lấy ra value (CHÚ Ý - VECTOR ở dạng cột)
plt.plot([0,ie * iv[0]], [0, ie * iv[1]], color = 'r', lw = 3)
plt.show()
1.1.1.7. Orthogonality and Orthonarmal Set#
(trực giao và trực chuẩn)
1. Trực giao: Bộ Vector trong không gian V mà từng vector đôi một có tích vô hướng = 0 (vuông góc với nhau)
2. Trực chuẩn: Là bộ vector trực giao và độ dài từng vector là vector đơn vị ( độ dài = 1)
Gram-schmidt: là proces tìm ra bộ vectỏ trực chuẩn/trực giao từ 1 hệ vector hữu hạn và độc lập tuyến tính
Việc tìm maxtrix ttrực giao/ trực chuẩn giúp hình thành 1 space mới tốt hơn từ vector đã có
Tích vô hướng của các vector sau khi xoay/chiếu sẽ không đổi
def gs(X, row_vecs=True, norm = True):
if not row_vecs:
X = X.T
Y = X[0:1,:].copy()
for i in range(1, X.shape[0]):
proj = np.diag((X[i,:].dot(Y.T)/np.linalg.norm(Y,axis=1)**2).flat).dot(Y)
Y = np.vstack((Y, X[i,:] - proj.sum(0)))
if norm:
Y = np.diag(1/np.linalg.norm(Y,axis=1)).dot(Y)
if row_vecs:
return Y
else:
return Y.T
gs(np.array([[2,1],[3,2]]))
array([[ 0.89442719, 0.4472136 ],
[-0.4472136 , 0.89442719]])
1.1.1.8. Hạng của matrix - low rank factorization#
Span: Không gian sinh, trong không gian n chiều, span được tạo bởi m vector độc lập tuyến tính (1<=m<=n)
Rank matrix: là số vector independent trong matrix đôi một, túc là số vector độc lập tuyến tính biểu diễn được tất các các vector trong matrix
rank(M) <= Số vector tạo ra matrix M
Với data matrix mxn có rank k, thể hiện k obs đặc trưng (k nhóm) và mỗi obs trong m obs là sự kết hợp tuyến tính của k obs đặc trưng
matrixA = np.array([[1, 2, 3, 23],
[4, 5, 6, 25],
[7, 8, 9, 28],
[10, 11, 12, 41]])
np.linalg.matrix_rank(matrixA)
3
1.1.1.8.1. low rank factorization#
Áp dụng cho bài toán xấp xỉ và gom nhóm, với số \(k < rank(A_{m.n})\), ta phân rã \(A_{m.n} \approx W_{m.k} x H_{k.n}\), khi đó tích của 2 matrix mới sẽ có rank = k, tức k nhóm được gom lại
1.1.2. Các loại khoảng cách#
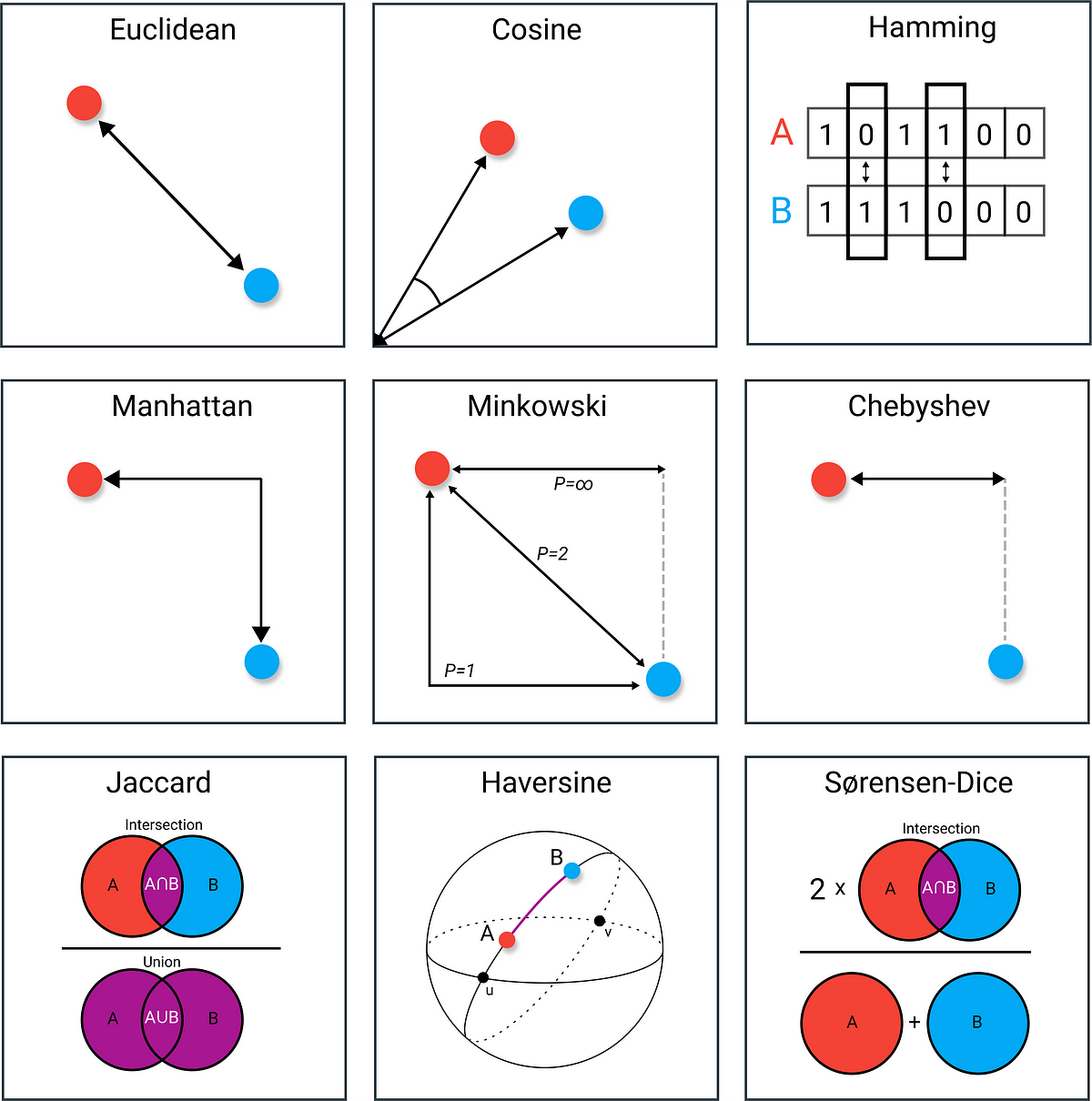
1. Euclidean
Khoảng cách này ko quan tâm độ dài từng trục mà chỉ quan tâm tới khoảng cách đường chéo
2. Manhattan
Quan tâm tới sụ sai khác trên từng trục
VD: bài toán gom nhóm KH theo tuổi và order. Nếu sử dụng euclidean thì KH tuổi nhỏ và order lớn có thể cùng nhóm với KH tuổi lớn và order nhỏ.
Nếu sử dụng manhattan thì quan tâm tới distance trên từng feature.
Nếu ko rõ được pp xác định k/c phù hợp thì nên sử dụng feature scaling trước.
3. Minkowski Khoảng cách nhỏ nhất theo 1 hướng nào đó
4. Chebychev Khoảng cách hình chiếu
5. Cosine Khoảng cách góc, phù hợp cho các bài toán recommendation system
6. Hamming Khoảng cách theo mức độ tương đồng, phù hợp với các bài toán NLP
1.1.3. Correlation#
1.1.3.1. Correlation#
1.1.3.1.1. Pearson#
Tính correlation áp dụng cho dữ liệu linear
# correlation of 2 arrays
np.correlate(A, B)
array([39793])
# correlation matrix
np.corrcoef(data)
array([[ 1. , 0.29815244, -0.19037969],
[ 0.29815244, 1. , -0.13043545],
[-0.19037969, -0.13043545, 1. ]])
1.1.3.2. Spearman#
Tính correlation theo rank ( tính rank của X trong sample rồi tính corr của các giá trị rank)
Spearman áp dụng trong TH dữ liệu non-linear, hoặc nghi ngờ tính chính xác của dữ liệu (dữ liệu ở dạng xấp xỉ hoặc là output của 1 model khác)
1.1.3.3. Covariance#

Covariance thể hiện tương quan của 2 biến, mà không bị giới hạn trong [-1,1] như correlation
import seaborn as sn
A = [45,37,42,35,39,1,5,55,7,4,7,54,21,12,45,7,8,85,52,42,45,55,12,47,22,23,75,1,45,7]
B = [38,31,26,28,33,11,37,32,41,42,73,85,37,12,32,12,77,78,63,47,25,21,2,66,55,45,45,32,1,3]
C = [10,15,17,21,12,44,23,3,35,34,63,36,52,25,75,57,41,42,43,36,26,52,86,68,69,72,27,17,82,93]
data = np.array([A,B,C])
covMatrix1 = np.cov(data,bias=False)
print(covMatrix1)
sn.heatmap(covMatrix1, annot=True, fmt='g')
# plt.show()
[[ 530.21264368 157.74712644 -107.91954023]
[ 157.74712644 527.95402299 -73.7816092 ]
[-107.91954023 -73.7816092 606.05057471]]
<AxesSubplot: >

