Overview Recommendation Evaluation

2.5.6.1. Overview Recommendation Evaluation#

Thường chứng ta sẽ care about những top ranked items, những item xếp hạng thấp thường ít có ý nghĩa vì không được sử dụng. Do đó, các phương pháp ML metrics thường ít liên quan trong hệ thống RS.

Các phương pháp đo lường trong RS:

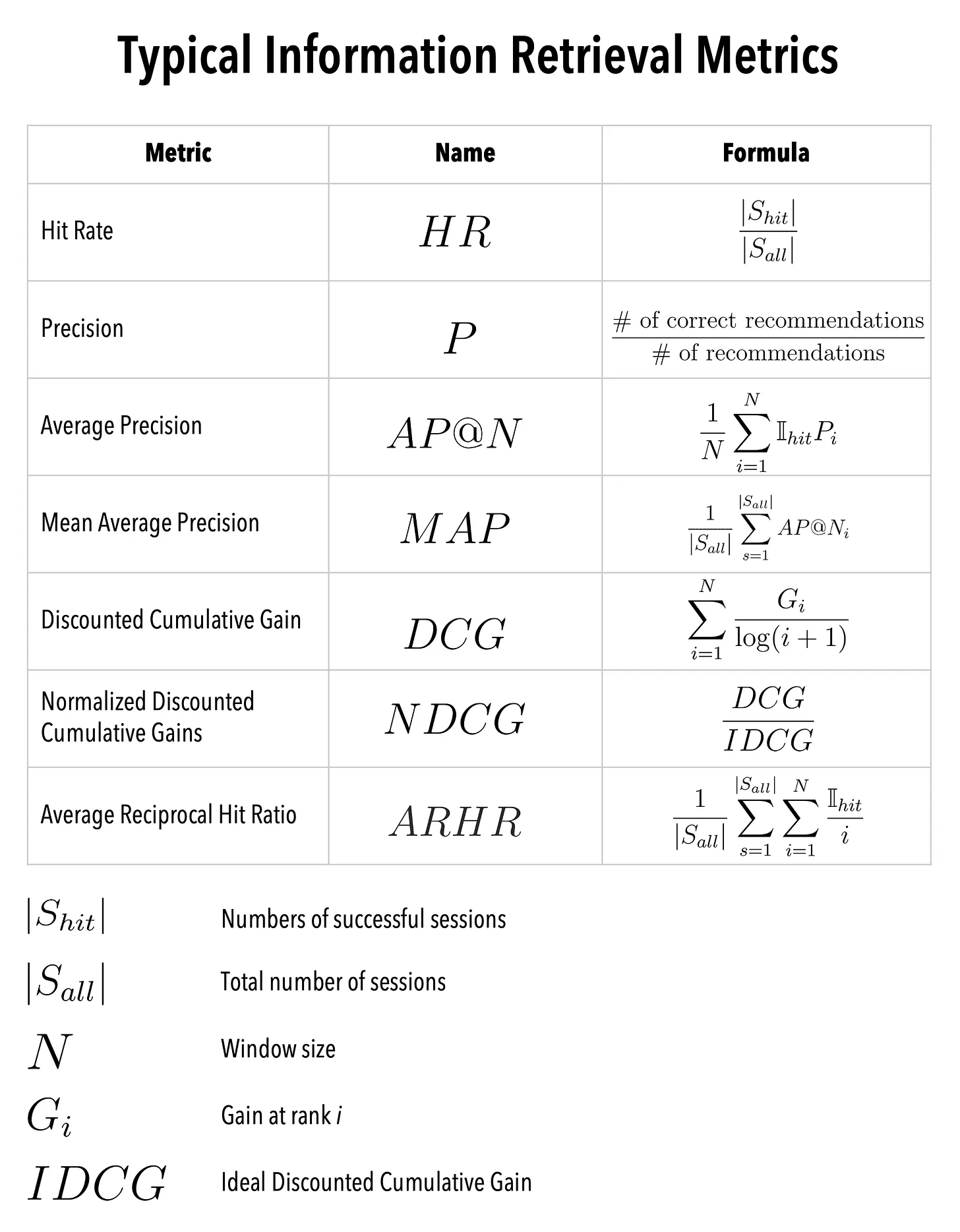
  • The hit rate

  • Precision and recall

  • The average precision (AP@N) and recall at N (AR@N)

  • The mean average precision (mAP@N) and the mean average recall at N (mAR@N)

  • The cumulative gains (CG)

  • The discounted cumulative gains (DCG)

  • The normalized discounted cumulative gains (NDCG)

  • The Kendall rank correlation coefficient

  • Average reciprocal hit rate

2.5.6.1.1. Labeling theory#

Trong hệ thống recommendation, phương pháp tiếp cận hybrid (regression + classification) thường được sử dụng

1. Regression (Score-based): Thường sử dụng khi dự đoán điểm rating (giá trị continuous)

Các metrics thường dùng

  • RMSE

  • MAE

Algorithms

  • Linear Regression

  • Matrix Factorization

  • Neural network

Lưu ý

  • data cần được chuẩn hoá normalized or standardized

2. Classification (Class-based): Nếu bài toán có mục tiêu cụ thể là phân loại like or dislike để recommend hoặc là choosing Top-N items để recommend

Note: Top-N Recommendation trong classification: khác với Top-N trong regression là predict score/rating sau đó chọn ra top N điểm cao nhất, thì với Top-N trong classification thì mới mỗi class sẽ phân loại item về class dựa trên xác suất, vựa chọn top-N item có xác suất cao nhât (tức là có item có thể thuộc nhiều class nếu nó cùng nằm trong Top-N của nhiều class khác nhau)

Label

  • like/dislike

  • click/no-click

  • class: 1-5 stars

2.5.6.1.2. Đánh giá độ chính xác của điểm rating dự đoán#

Đánh giá độ chính xác của điểm thường sử dụng các metrics của regression

  1. Root Mean Squared Error (RMSE)

  2. Mean Absolute Error (MAE)

  3. R-Squared (R²)

RMSE, MAE, R²: Là các chỉ số đo lường sai số trong các bài toán dự đoán liên tục (như dự đoán rating), thường được sử dụng để đánh giá độ lệch giữa giá trị dự đoán và giá trị thực tế.

2.5.6.1.2.1. Root Mean Squared Error (RMSE)#

Định Nghĩa và Cách Đánh Giá

Root Mean Squared Error (RMSE) là chỉ số đánh giá mức độ sai lệch giữa giá trị dự đoán và giá trị thực tế, bằng cách tính căn bậc hai của trung bình cộng bình phương sai số. RMSE cung cấp một thước đo tổng quát về sự chính xác của các dự đoán, với các sai số lớn đóng góp nhiều hơn vào giá trị cuối cùng do việc bình phương sai số.

Khi Nào Sử Dụng

RMSE thường được sử dụng để đánh giá các mô hình dự đoán giá trị số, chẳng hạn như trong hệ thống recommendation system dạng rating, nơi bạn muốn đánh giá mức độ gần đúng của các dự đoán so với rating thực tế của người dùng. Đây là chỉ số hữu ích khi bạn cần một thước đo tổng thể cho độ chính xác của dự đoán.

Công Thức

RMSE được tính bằng công thức:

\[ \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} ( \hat{y}_i - y_i )^2} \]

Trong đó:

  • N là tổng số điểm dữ liệu.

  • \(\hat{y}_i\) là giá trị dự đoán.

  • \(y_i\) là giá trị thực tế.

Lưu Ý

  • RMSE nhấn mạnh vào các lỗi lớn do việc bình phương sai số, vì vậy rất nhạy cảm với các dự đoán sai lầm lớn.

  • Đơn vị của RMSE giống với đơn vị của các giá trị cần dự đoán, giúp dễ dàng diễn giải kết quả.

from sklearn.metrics import mean_squared_error
import numpy as np # type: ignore

y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]

rmse = np.sqrt(mean_squared_error(y_true, y_pred))
print(f"RMSE: {rmse}")

RMSE: 0.6123724356957945

2.5.6.1.2.2. Mean Absolute Error (MAE)#

Định Nghĩa và Cách Đánh Giá

Mean Absolute Error (MAE) đo lường sai số trung bình giữa giá trị dự đoán và giá trị thực tế, bằng cách tính trung bình của các giá trị tuyệt đối của sai số. MAE cung cấp một thước đo đơn giản và dễ hiểu về độ lệch trung bình giữa các dự đoán và giá trị thực tế, không bị ảnh hưởng quá nhiều bởi các sai số lớn.

Khi Nào Sử Dụng

MAE được sử dụng phổ biến trong các bài toán dự đoán liên tục, nơi cần đánh giá độ lệch trung bình giữa dự đoán và thực tế mà không quá nhấn mạnh vào các sai số lớn. MAE là chỉ số hữu ích khi bạn muốn có một cái nhìn tổng quan về sai số mà không bị chi phối bởi các giá trị sai lệch cực đoan.

Công Thức

MAE được tính bằng công thức:

\[ \text{MAE} = \frac{1}{N} \sum_{i=1}^{N} \left| \hat{y}_i - y_i \right| \]

Trong đó:

  • N là tổng số điểm dữ liệu.

  • \(\hat{y}_i\) là giá trị dự đoán.

  • \(y_i\) là giá trị thực tế.

Lưu Ý

  • MAE ít nhạy cảm hơn với các lỗi lớn so với RMSE do không có phép bình phương.

  • MAE dễ diễn giải hơn trong ngữ cảnh của nhiều ứng dụng thực tế vì nó đo lường độ lệch trung bình mà không làm tăng quá mức ảnh hưởng của các sai số lớn.

from sklearn.metrics import mean_absolute_error

y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]

mae = mean_absolute_error(y_true, y_pred)
print(f"MAE: {mae}")

MAE: 0.5

2.5.6.1.2.3. R-Squared (R²)#

Định Nghĩa và Cách Đánh Giá

R-Squared (R²), còn được gọi là hệ số xác định, đo lường tỷ lệ phương sai của biến phụ thuộc (y) được giải thích bởi biến độc lập (x) trong mô hình. Nó cho biết mức độ phù hợp của mô hình với dữ liệu, cho thấy phần trăm biến động của biến phụ thuộc được mô hình giải thích.

Khi Nào Sử Dụng

R² được sử dụng phổ biến trong các mô hình hồi quy, bao gồm cả hệ thống recommendation, khi cần đánh giá mức độ mô hình giải thích được dữ liệu. Chỉ số này giúp đánh giá sự phù hợp của mô hình trong việc dự đoán các giá trị dựa trên các biến độc lập.

Công Thức

R² được tính bằng công thức:

\[ R^2 = 1 - \frac{\sum_{i=1}^{N} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{N} (y_i - \bar{y})^2} \]

Trong đó:

  • \(\bar{y}\) là giá trị trung bình của \(y_i\).

  • \(y_i\) là giá trị thực tế.

  • \(\hat{y}_i\) là giá trị dự đoán.

Lưu Ý

  • R² có thể nằm trong khoảng từ 0 đến 1, với giá trị 1 cho thấy mô hình giải thích hoàn toàn phương sai của dữ liệu.

  • R² có thể âm nếu mô hình rất tệ, nghĩa là mô hình đó dự đoán kém hơn so với trung bình của giá trị thực tế.

from sklearn.metrics import r2_score

y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]

r2 = r2_score(y_true, y_pred)
print(f"R²: {r2}")

R²: 0.9486081370449679

2.5.6.1.3. Recommendation rank metrics#

2.5.6.1.3.1. Traditional classification metrics#

  1. Precision: Đánh giá tỷ lệ tỷ lệ dự đoán đúng trong danh sách dự đoán

  2. Recall: Đánh giá tỷ lệ dự đoán đúng trong danh sách đúng thực tế.

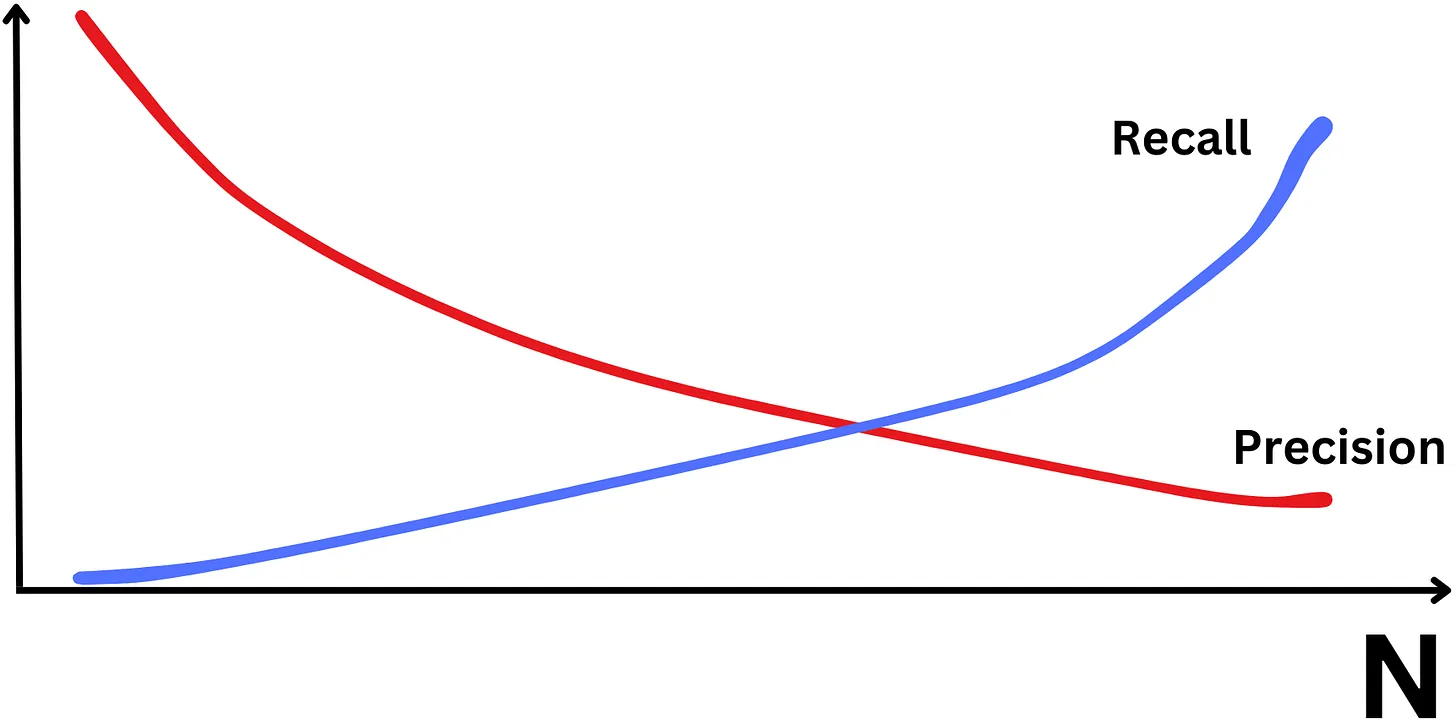
  3. F1-Score: Cân bằng giữa Recall và Precision để lựa chọn ra window K phù hợp.

Khi tăng K thì Recall tăng nhưng Precision giảm và ngược lại

  1. Area Under Curve - Receiver Operating Characteristic (AUC-ROC): Được sử dụng khi bạn muốn đánh giá khả năng phân biệt của mô hình giữa các lớp khác nhau, phù hợp cho các hệ thống recommendation có phân loại nhị phân.

Trong thực tế, chúng ta thường quan tâm đến độ chính xác (Yêu thích = True) những items top đầu K thay vì khả năng phân loại tổng thể của model. Do đó các traditional classification metrics sẽ được điều chỉnh để phù hợp hơn vs bài toán recommendation

2.5.6.1.3.1.1. Precision@K#

Định Nghĩa và Cách Đánh Giá

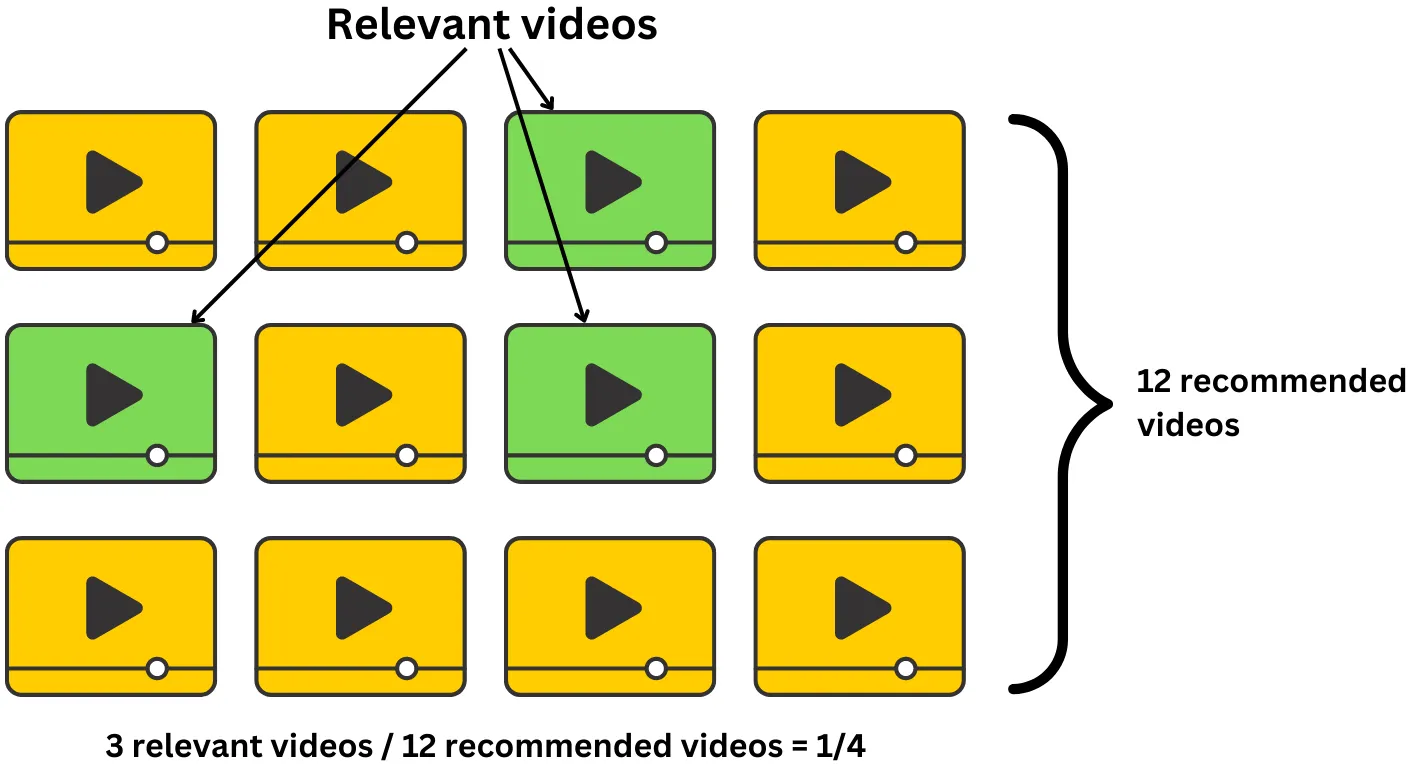
Precision@K là một chỉ số đánh giá quan trọng trong các hệ thống gợi ý (recommendation systems). Nó đo lường tỷ lệ phần trăm các mục trong danh sách gợi ý ở vị trí đầu tiên mà người dùng thực sự quan tâm hoặc thấy chúng phù hợp.

Khi Nào Sử Dụng

Precision@K đặc biệt hữu ích khi bạn muốn đảm bảo rằng những mục đầu tiên trong danh sách gợi ý là những mục có khả năng cao để người dùng thích hoặc quan tâm. Điều này rất quan trọng trong các tình huống mà người dùng chỉ xem xét các mục ở đầu danh sách, chẳng hạn như trong các nền tảng mua sắm, phát trực tuyến video, hay tìm kiếm thông tin.

Công Thức

\[ \text{Precision@K} = \frac{\text{Số lượng dự đoán chính xác trong K}}{K} \]

Trong đó:

  • Số lượng dự đoán chính xác trong K là số lượng dự đoán đúng nằm trong số K dự đoán hàng đầu mà hệ thống cung cấp.

  • K là số lượng kết quả hàng đầu mà bạn đang xem xét.

Ví dụ:

Giả sử bạn đang đánh giá một hệ thống gợi ý với K = 5. Nếu trong 5 gợi ý hàng đầu của hệ thống, có 3 gợi ý là chính xác, thì Precision@5 sẽ được tính như sau:

\[ \text{Precision@5} = \frac{3}{5} = 0.6 \]

Điều này có nghĩa là 60% trong số các gợi ý hàng đầu là chính xác.

Lưu Ý

  • Precision@K chỉ quan tâm đến K mục đầu tiên và không xét đến thứ tự của các mục trong danh sách sau đó.

  • Giá trị của \(K\) cần được chọn sao cho phù hợp với mục tiêu của hệ thống gợi ý hoặc yêu cầu của bài toán cụ thể.

def precision_at_k(recommended_items, relevant_items, k):
    recommended_k = recommended_items[:k]
    num_relevant = len(set(recommended_k) & set(relevant_items))
    return num_relevant / k

recommended_items = [1, 2, 3, 4, 5]
relevant_items = [3, 4, 7]
k = 3

precision = precision_at_k(recommended_items, relevant_items, k)
print(f"Precision@{k}: {precision}")

Precision@3: 0.3333333333333333

2.5.6.1.3.1.2. Recall@K#

Định Nghĩa và Cách Đánh Giá

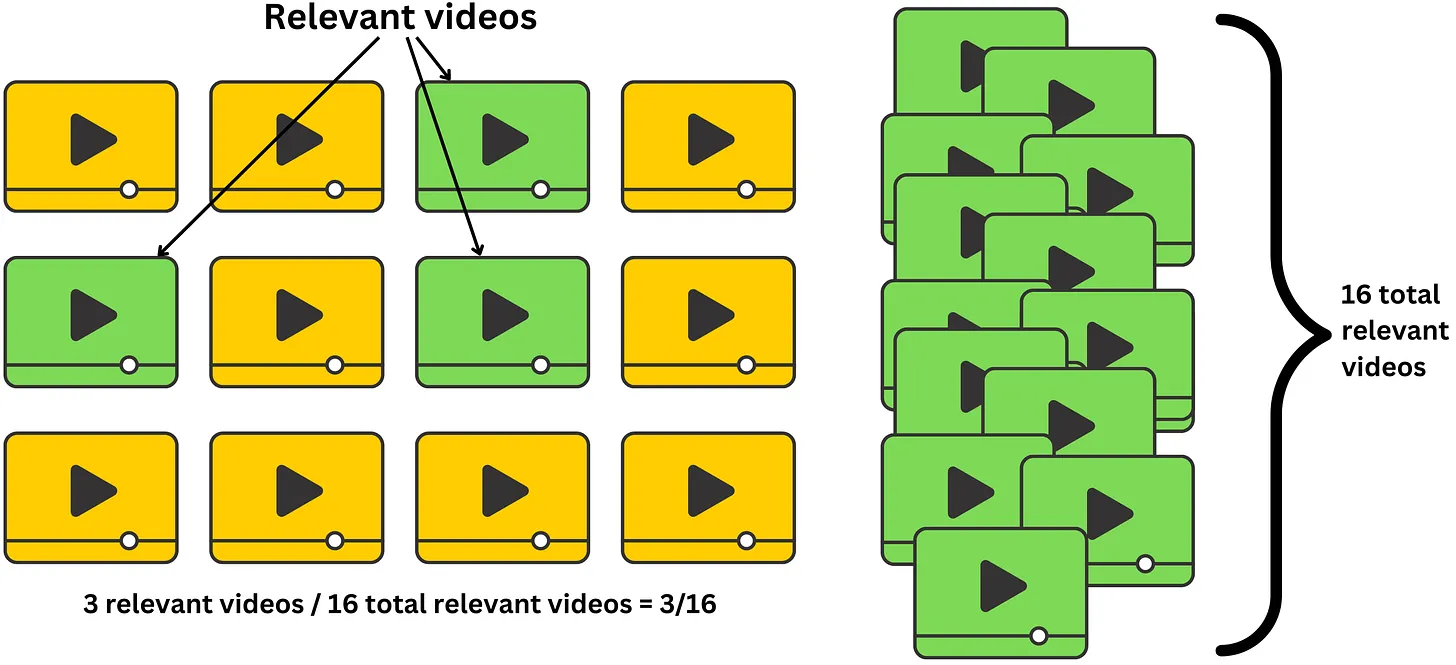
Recall@K đo lường tỷ lệ các mục liên quan (relevant items) được đề xuất trong top K mục so với tổng số mục liên quan thực tế. Đây là một chỉ số quan trọng để đánh giá khả năng của hệ thống trong việc tìm ra tất cả các mục mà người dùng quan tâm.

Khi Nào Sử Dụng

Recall@K được sử dụng khi mục tiêu là tối ưu hóa việc phát hiện tất cả các mục mà người dùng quan tâm, thay vì chỉ tập trung vào độ chính xác của những mục đầu tiên. Đây là chỉ số hữu ích trong các hệ thống gợi ý hoặc tìm kiếm nơi bạn muốn đảm bảo rằng các mục liên quan quan trọng không bị bỏ sót.

Công Thức

Recall@K được tính bằng công thức:

\[ \text{Recall@K} = \frac{\text{Số lượng mục liên quan trong top K}}{\text{Tổng số mục liên quan}} \]

Trong đó:

  • Số lượng mục liên quan trong top K là số lượng mục liên quan được tìm thấy trong danh sách top K gợi ý.

  • Tổng số mục liên quan là số lượng tất cả các mục liên quan thực tế trong toàn bộ tập dữ liệu.

Lưu Ý

  • Recall@K không quan tâm đến thứ tự của các mục được đề xuất; nó chỉ tập trung vào việc có bao nhiêu mục liên quan được tìm thấy trong số K mục hàng đầu.

  • Đối với các tập dữ liệu lớn, việc tăng K sẽ làm tăng giá trị Recall nhưng có thể dẫn đến sự giảm sút trong Precision, vì số lượng gợi ý không chính xác có thể gia tăng.

def recall_at_k(recommended_items, relevant_items, k):
    recommended_k = recommended_items[:k]
    num_relevant = len(set(recommended_k) & set(relevant_items))
    return num_relevant / len(relevant_items)

recommended_items = [1, 2, 3, 4, 5]
relevant_items = [3, 4, 7]
k = 3

recall = recall_at_k(recommended_items, relevant_items, k)
print(f"Recall@{k}: {recall}")

Recall@3: 0.3333333333333333

2.5.6.1.3.1.3. F1-Score#

Định Nghĩa và Cách Đánh Giá

F1-Score là trung bình điều hòa của Precision và Recall, cân bằng giữa việc không bỏ sót (Recall) và không gán sai (Precision). Chỉ số này đặc biệt hữu ích trong các bài toán phân loại nhị phân, nơi bạn cần cân bằng giữa việc phát hiện tất cả các mục liên quan và giảm thiểu các lỗi gán nhãn.

Khi Nào Sử Dụng

F1-Score được sử dụng khi bạn cần cân bằng giữa Precision và Recall, đặc biệt trong các trường hợp có sự mất cân bằng giữa các lớp dữ liệu. Đây là chỉ số quan trọng khi cả hai yếu tố Precision và Recall đều quan trọng đối với chất lượng của mô hình.

Thực tế, trong bài toán recommendation, thường sẽ ưu tiên tối đa hoá Precision hơn là Recall, tức là K thường thấp để đảm bảo các items trong recommend list có khả năng cao sẽ phù hợp, hơn là tìm kiếm được tất cả các item ưa thích kèm theo rất nhiều các item ko ưa thích.

Công Thức

F1-Score được tính bằng công thức:

\[ \text{F1-Score} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} \]

Trong đó:

  • Precision là tỷ lệ các dự đoán chính xác so với tổng số dự đoán.

  • Recall là tỷ lệ các mục liên quan được phát hiện so với tổng số mục liên quan thực tế.

Lưu Ý

  • F1-Score quan trọng trong các tình huống cần tối ưu hóa đồng thời Precision và Recall.

  • Giá trị F1-Score cao chỉ đạt được khi cả Precision và Recall đều cao, cho thấy mô hình không chỉ chính xác mà còn có khả năng phát hiện hầu hết các mục liên quan.

from sklearn.metrics import f1_score

y_true = [0, 1, 1, 1, 0, 1]
y_pred = [0, 1, 0, 1, 0, 1]

f1 = f1_score(y_true, y_pred)
print(f"F1-Score: {f1}")

F1-Score: 0.8571428571428571

2.5.6.1.3.1.4. Area Under Curve - Receiver Operating Characteristic (AUC-ROC)#

Định Nghĩa và Cách Đánh Giá

AUC-ROC là chỉ số đo lường khả năng phân biệt giữa các lớp của mô hình phân loại. ROC là đồ thị giữa tỷ lệ True Positive Rate (TPR) và False Positive Rate (FPR), trong khi AUC là diện tích dưới đường cong ROC. Chỉ số AUC cho biết khả năng của mô hình trong việc phân biệt giữa các lớp.

Khi Nào Sử Dụng

AUC-ROC được sử dụng để đánh giá hiệu suất của các mô hình phân loại, đặc biệt trong trường hợp dữ liệu bị mất cân bằng giữa các lớp. Nó rất hữu ích khi bạn cần một chỉ số tổng quát để đánh giá khả năng phân biệt của mô hình mà không bị ảnh hưởng bởi sự phân bố lớp không đều.

Công Thức

AUC-ROC không có công thức đơn giản, nó được tính toán bằng cách lấy diện tích dưới đường cong ROC. Đường cong ROC được tạo ra bằng cách vẽ tỷ lệ True Positive Rate (TPR) so với tỷ lệ False Positive Rate (FPR) cho các ngưỡng khác nhau.

Lưu Ý

  • AUC-ROC là một thước đo toàn diện, cho thấy khả năng mô hình phân biệt giữa các lớp.

  • Giá trị AUC gần 1 chỉ ra mô hình tốt, trong khi giá trị gần 0.5 cho thấy mô hình không có khả năng phân biệt (hoạt động ngẫu nhiên).

2.5.6.1.3.2. Mean Average Precision (mAP@N) and Mean Average Recall at N (mAR@N)#

Thay vì đánh giá nhiều window K, thì chúng ta có thể đánh giá tất cả các window K có thể, phù hợp khi ko cố định được Window K.

Khi đó, các vị trí càng xa trong list recommendation sẽ có trọng số càng thấp trong việc đánh giá. Chúng ta chỉ xét Precision và Recall tại N top item

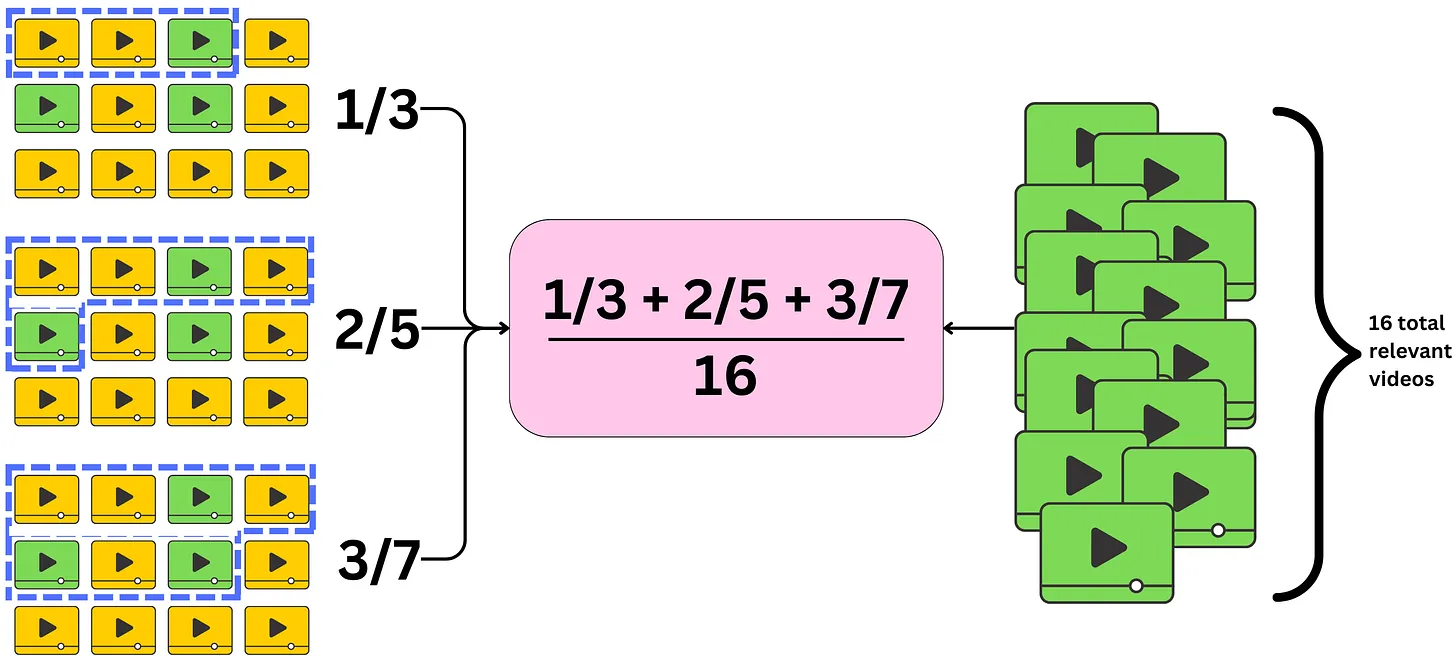
2.5.6.1.3.2.1. Average Precision at N (AP@N)#

AP@N answers the questions of what is the average precision for any window size

We still consider the maximum window size K, but we also consider all the window sizes k within it where there is a relevant item: $\( \text{AP@N}=\frac{1}{\text{\# total relevant items}}\sum_{k=1}^N\text{Precision@}k \text{ if kth item relevant} \)$

  • We only include the precision in the sum if the item is relevant for that window size

  • For each user, we average those precisions and normalize by the number of relevant items

2.5.6.1.3.2.2. Average Recall at N (AR@N)#

AR@N answers the questions of What is the average recall for any window size

Similar with the way calculate the AP@N, but the fomular of AR@N: $\( \text{AR@N}=\frac{1}{\text{\# total relevant items}}\sum_{k=1}^N\text{Recall@}k \text{ if kth item relevant} \)$

  • We only include the recall in the sum if the item is relevant for that window size

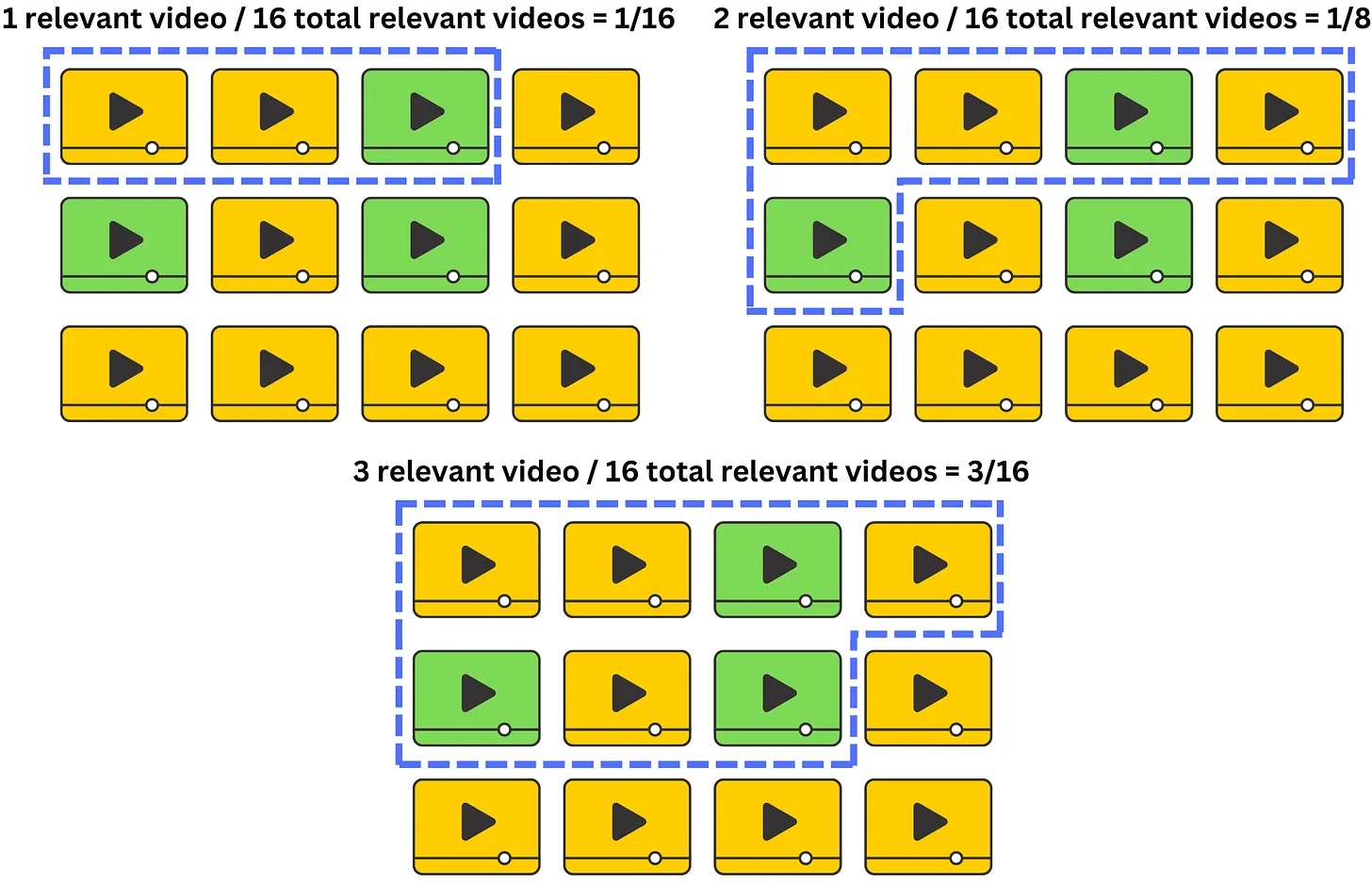
  • For each user, we average those recall and normalize by the number of relevant items

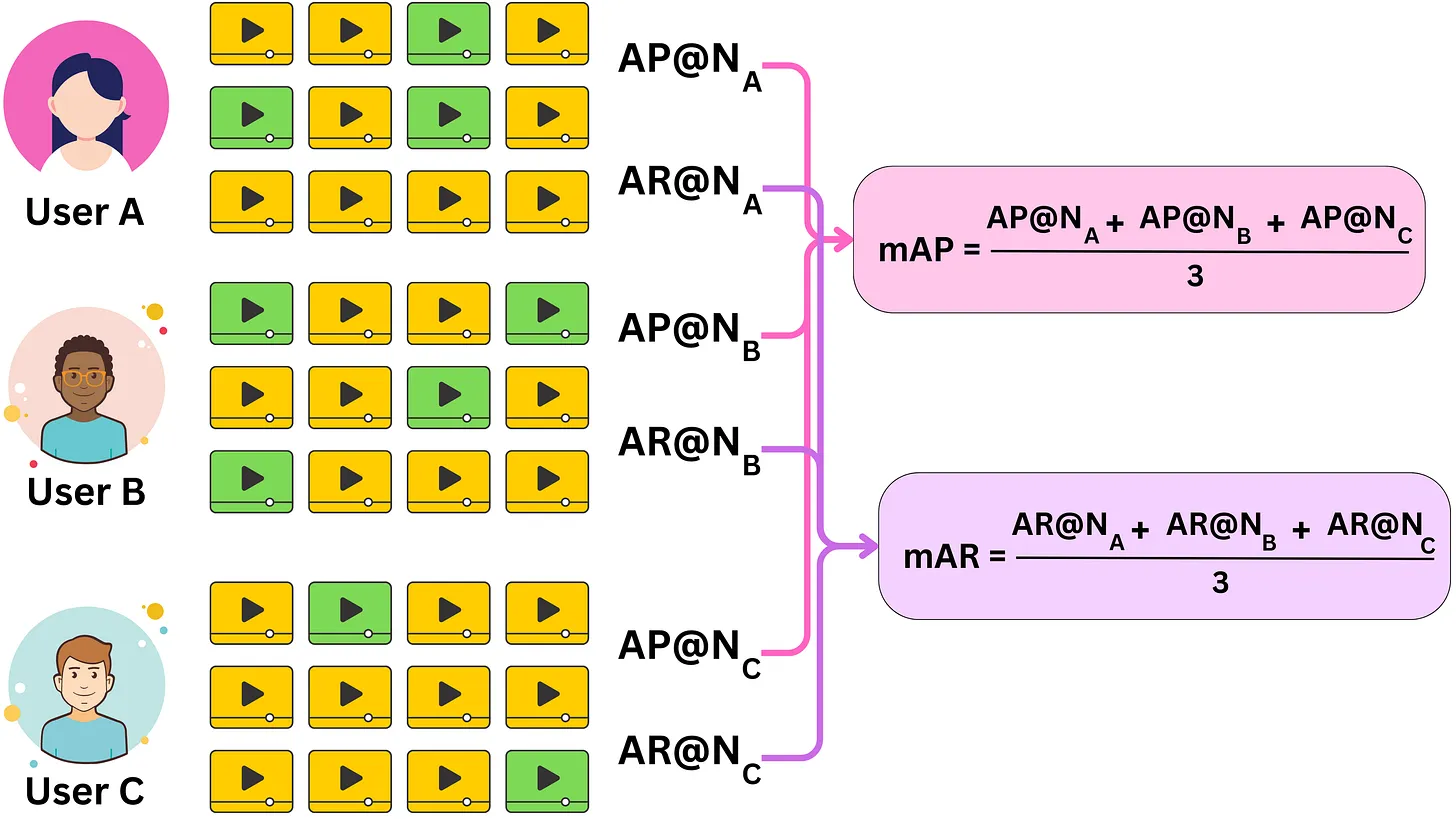
2.5.6.1.3.2.3. mAP@N and mAR@N#

Khi nhắc về mAP@N hoặc mAR@N thì:

  • mean(m): thể hiện average cross all the users

  • Average(A): thể hiện average cross all the different window sizes

\[ \text{mAP@N} = \frac{1}{\text{\# of users}}\sum_{i=1}^UAP@N \text{ for user }i \]
\[ \text{mAR@N} = \frac{1}{\text{\# of users}}\sum_{i=1}^UAR@N \text{ for user }i \]

2.5.6.1.3.3. Kendall rank correlation coefficient (KRCC)#

Phương pháp đo lường hệ số tương quan theo Kendall rank giữa giá trị dự đoán và giá trị thực tế.

Với mỗi 1 user:

  • ta có danh sách recommended list (k items) và relevant score từng item, tổng số cặp 2 item đôi một là k(k-1)/2

  • Xét từng pair, nếu thứ tự position 2 item đó đúng thì được xét là 1 cặp đúng, nếu không thì là 1 cặp sai

  • Công thức tính Kendall rank coefficient: $\( \tau=\frac{\text{\# number of pairs ordered correctly}-\text{\# number of pairs ordered incorrectly} }{\text{total number of pairs}} \)$

Tính giá trị KRCC cho all users

2.5.6.1.3.4. Mean Average Precision (MAP)#

Định Nghĩa và Cách Đánh Giá

Mean Average Precision (MAP) là trung bình cộng của các giá trị Average Precision (AP) cho tất cả các người dùng hoặc queries. AP là trung bình cộng của Precision tính trên tất cả các vị trí mà một mục liên quan xuất hiện trong danh sách đề xuất. MAP cung cấp cái nhìn tổng quát về chất lượng của hệ thống recommendation qua việc kết hợp độ chính xác và thứ hạng của các mục liên quan.

Khi Nào Sử Dụng

MAP được sử dụng để đánh giá tổng thể chất lượng của mô hình recommendation system trên toàn bộ tập người dùng, đặc biệt hữu ích khi bạn cần so sánh hiệu suất của các mô hình trên nhiều người dùng hoặc queries khác nhau. Chỉ số này giúp đo lường khả năng của hệ thống trong việc cung cấp các gợi ý có liên quan và chính xác.

Công Thức

  • Average Precision (AP) được tính bằng công thức:

\[ AP = \frac{1}{|R|} \sum_{k=1}^{N} P(k) \cdot \delta(k) \]

  • Mean Average Precision (MAP) được tính bằng công thức:

\[ MAP = \frac{1}{|Q|} \sum_{i=1}^{|Q|} AP_i \]

Trong đó:

  • P(k) là Precision tại vị trí k.

  • \(\delta(k)\) là hàm chỉ thị (bằng 1 nếu mục ở vị trí k là liên quan, ngược lại là 0).

  • R là số lượng mục liên quan.

  • Q là tổng số queries hoặc người dùng.

Lưu Ý

  • MAP tổng hợp thông tin từ Precision và tính đến thứ hạng của các mục liên quan, là một chỉ số toàn diện để đánh giá hệ thống.

  • Chỉ số này phù hợp khi tập dữ liệu có nhiều queries hoặc người dùng và bạn muốn đánh giá tổng thể hiệu suất của mô hình trên toàn bộ tập dữ liệu.

def average_precision(recommended_items, relevant_items):
    hits = 0
    sum_precision = 0.0
    for i, item in enumerate(recommended_items):
        if item in relevant_items:
            hits += 1
            sum_precision += hits / (i + 1)
    return sum_precision / len(relevant_items)

def mean_average_precision(recommendations, relevant_items_list):
    ap_sum = 0.0
    for recommended_items, relevant_items in zip(recommendations, relevant_items_list):
        ap_sum += average_precision(recommended_items, relevant_items)
    return ap_sum / len(recommendations)

recommendations = [[1, 2, 3, 4, 5], [2, 3, 4, 5, 6]]
relevant_items_list = [[3, 4, 7], [2, 6]]

map_score = mean_average_precision(recommendations, relevant_items_list)
print(f"MAP: {map_score}")

MAP: 0.4888888888888888

2.5.6.1.3.5. Mean Reciprocal Rank (MRR)#

Định Nghĩa và Cách Đánh Giá

Mean Reciprocal Rank (MRR) đo lường thứ hạng của mục liên quan đầu tiên trong danh sách các mục được đề xuất. Chỉ số này tính trung bình nghịch đảo của thứ hạng vị trí đầu tiên của các mục liên quan, cung cấp cái nhìn về việc các mục quan trọng được xếp hạng cao như thế nào trong danh sách đề xuất.

Khi Nào Sử Dụng

MRR rất hữu ích khi bạn muốn đảm bảo rằng các mục liên quan được đưa lên vị trí cao trong danh sách đề xuất. Chỉ số này giúp đánh giá tính hiệu quả của hệ thống trong việc ưu tiên các mục quan trọng và liên quan nhất.

Công Thức

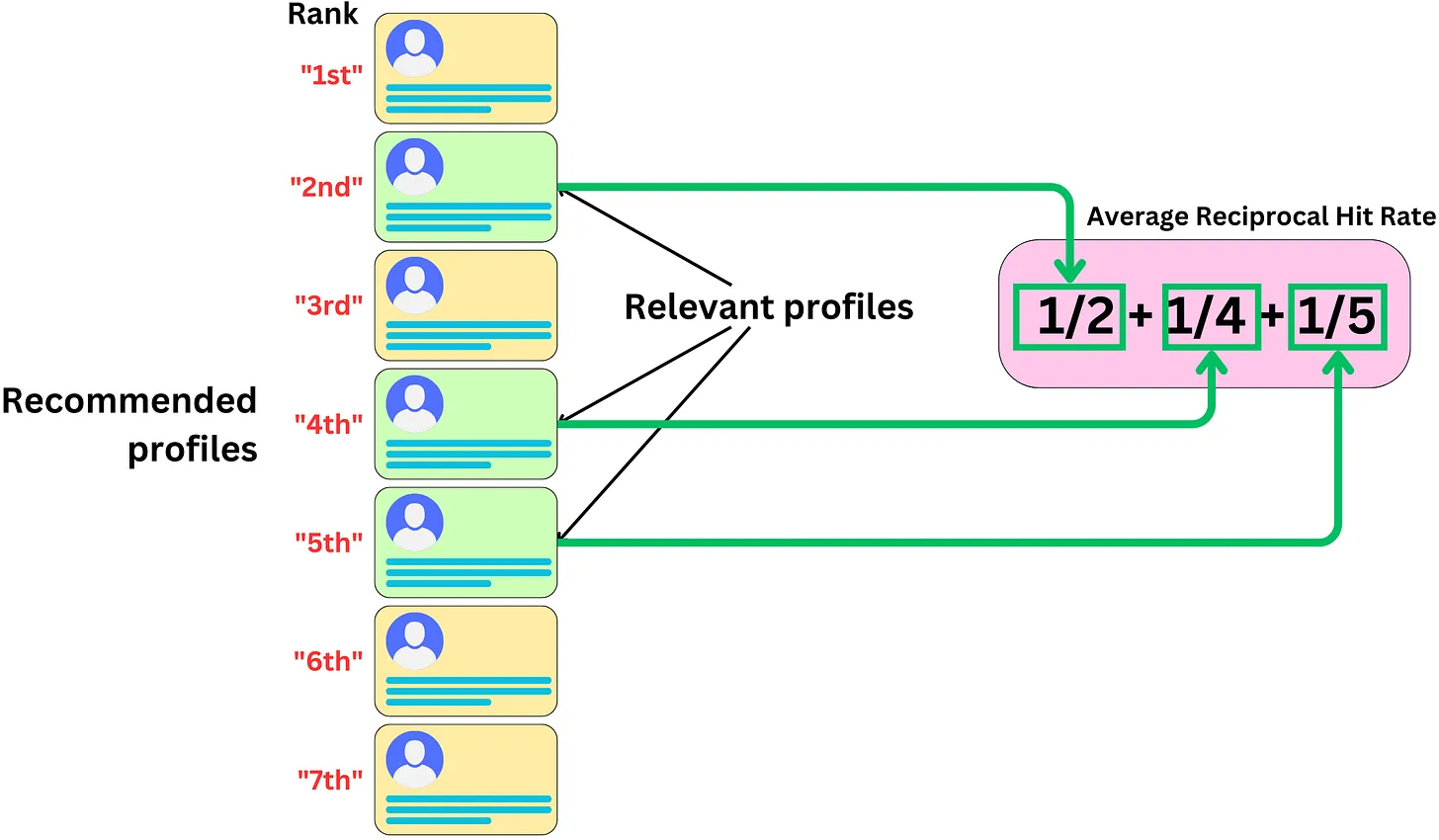
MRR được tính bằng công thức:

\[ MRR = \frac{1}{Q} \sum_{user=1}^{Q} \sum_{item=1}^{K} \frac{1}{\text{rank}_{item}} \]

Trong đó:

  • \(\text{rank}_i\) là thứ hạng của mục liên quan đầu tiên trong danh sách đề xuất của query i.

  • Q là tổng số người dùng.

Lưu Ý

  • Nếu không có mục liên quan nào trong danh sách đề xuất, thì Reciprocal Rank sẽ là 0.

  • Trong nhiều trường hợp thì ta có thể biến đổi MRR thành chỉ xét đến relevant item có position cao nhất trong recommended list, khi đó MRR nhạy cảm với thứ hạng của mục liên quan đầu tiên, nên rất hữu ích khi cần đánh giá tính chính xác của vị trí đầu tiên trong danh sách đề xuất.

def mean_reciprocal_rank(recommended_items, relevant_items):
    for rank, item in enumerate(recommended_items, start=1):
        if item in relevant_items:
            return 1 / rank
    return 0

recommended_items = [1, 2, 3, 4, 5]
relevant_items = [3, 4, 7]

mrr = mean_reciprocal_rank(recommended_items, relevant_items)
print(f"MRR: {mrr}")

MRR: 0.3333333333333333

2.5.6.1.3.6. Normalized Discounted Cumulative Gain (NDCG)#

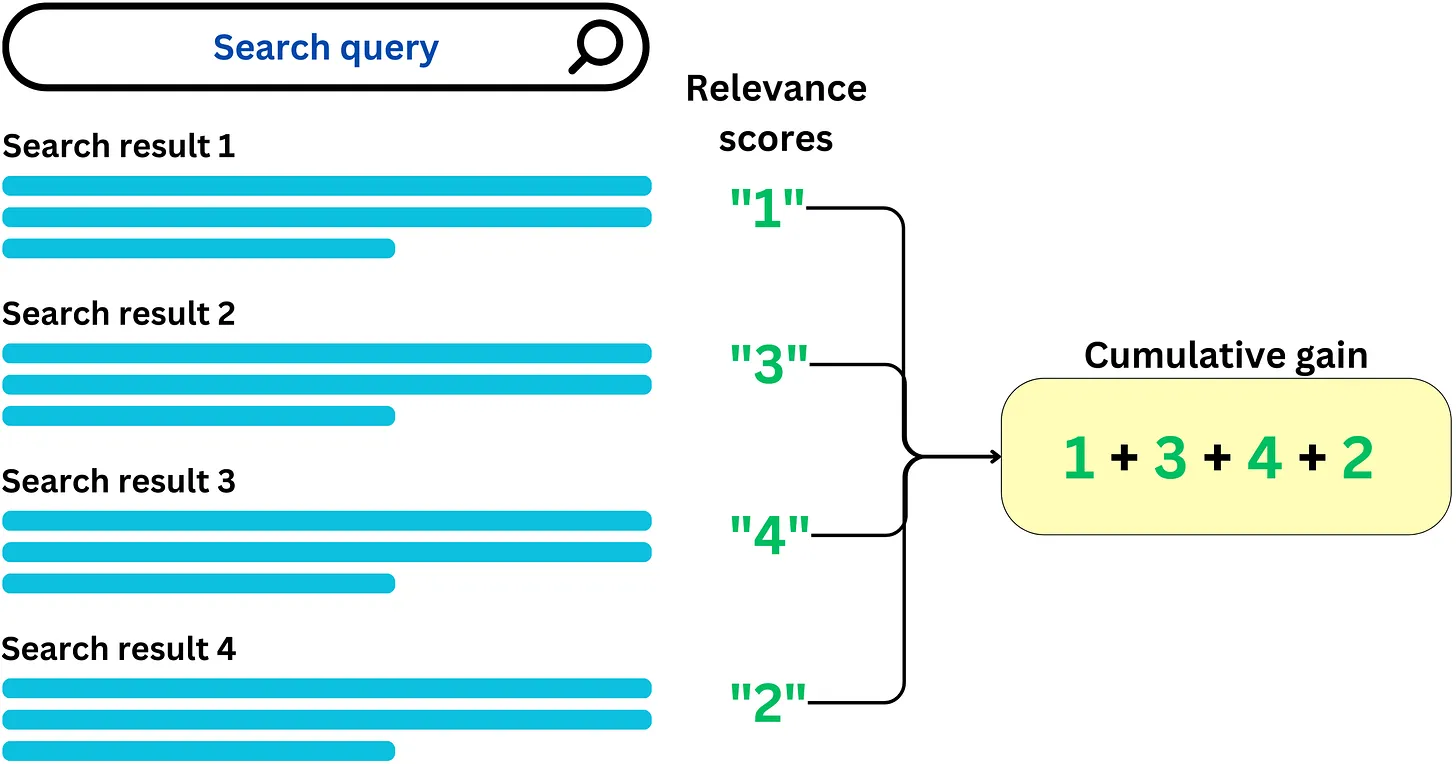
2.5.6.1.3.6.1. Step 1: Cumulative gain (CG)#

CG answer the question is how much relevance is contained in the recommended list $\( CG=\sum_{i=1}^N\text{relevance score}_i \)$

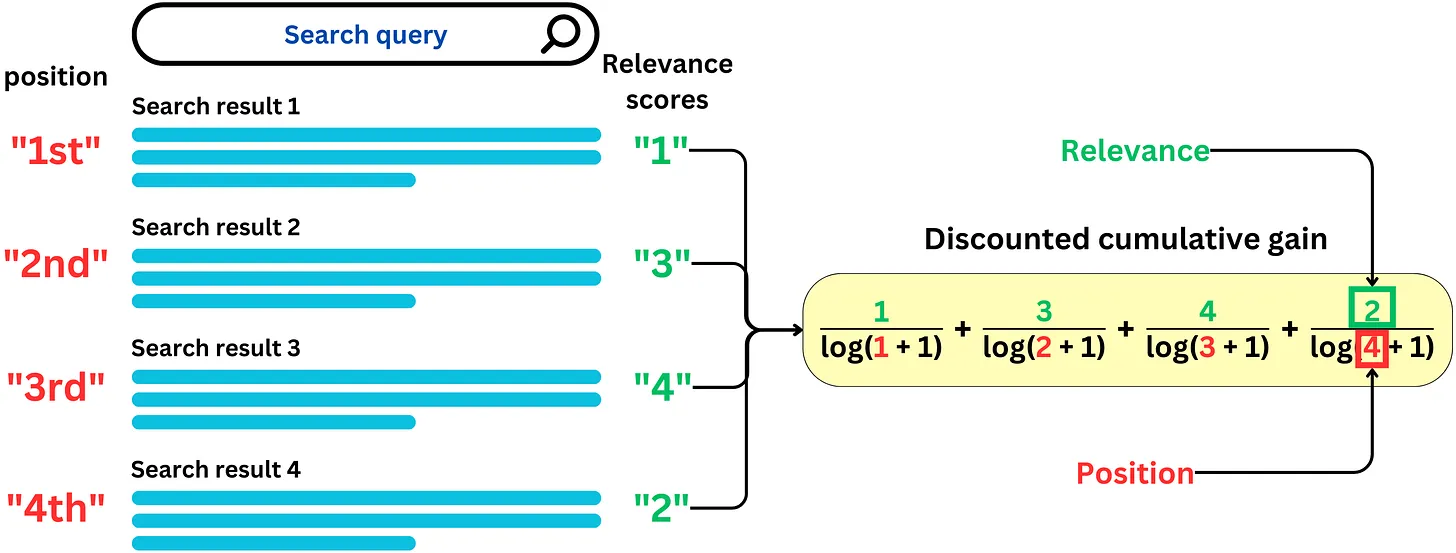
2.5.6.1.3.6.2. Step 2: Discounted cumulative gain (DCG)#

Thêm trọng số cho các score bằng thứ tự position của nó $\( DCG=\sum_{i=1}^N\frac{\text{relevance score}_i}{\log\left(i + 1\right)} \)$

2.5.6.1.3.6.3. Step 3: Normalized discounted cumulative gain (NDCG)#

Định Nghĩa và Cách Đánh Giá

Normalized Discounted Cumulative Gain (NDCG) đo lường chất lượng của danh sách đề xuất dựa trên vị trí của các mục liên quan, với các mục được xếp hạng cao hơn sẽ có giá trị lớn hơn. NDCG giúp đánh giá không chỉ sự hiện diện của các mục liên quan mà còn cả thứ hạng của chúng trong danh sách đề xuất, phản ánh chính xác hơn chất lượng của hệ thống.

Khi Nào Sử Dụng

NDCG được sử dụng khi cần đánh giá không chỉ sự hiện diện của các mục liên quan mà còn cả thứ hạng của chúng trong danh sách đề xuất. Đây là chỉ số hữu ích khi bạn muốn đảm bảo rằng các mục quan trọng được xếp hạng cao hơn trong danh sách kết quả tìm kiếm hoặc gợi ý.

Công Thức

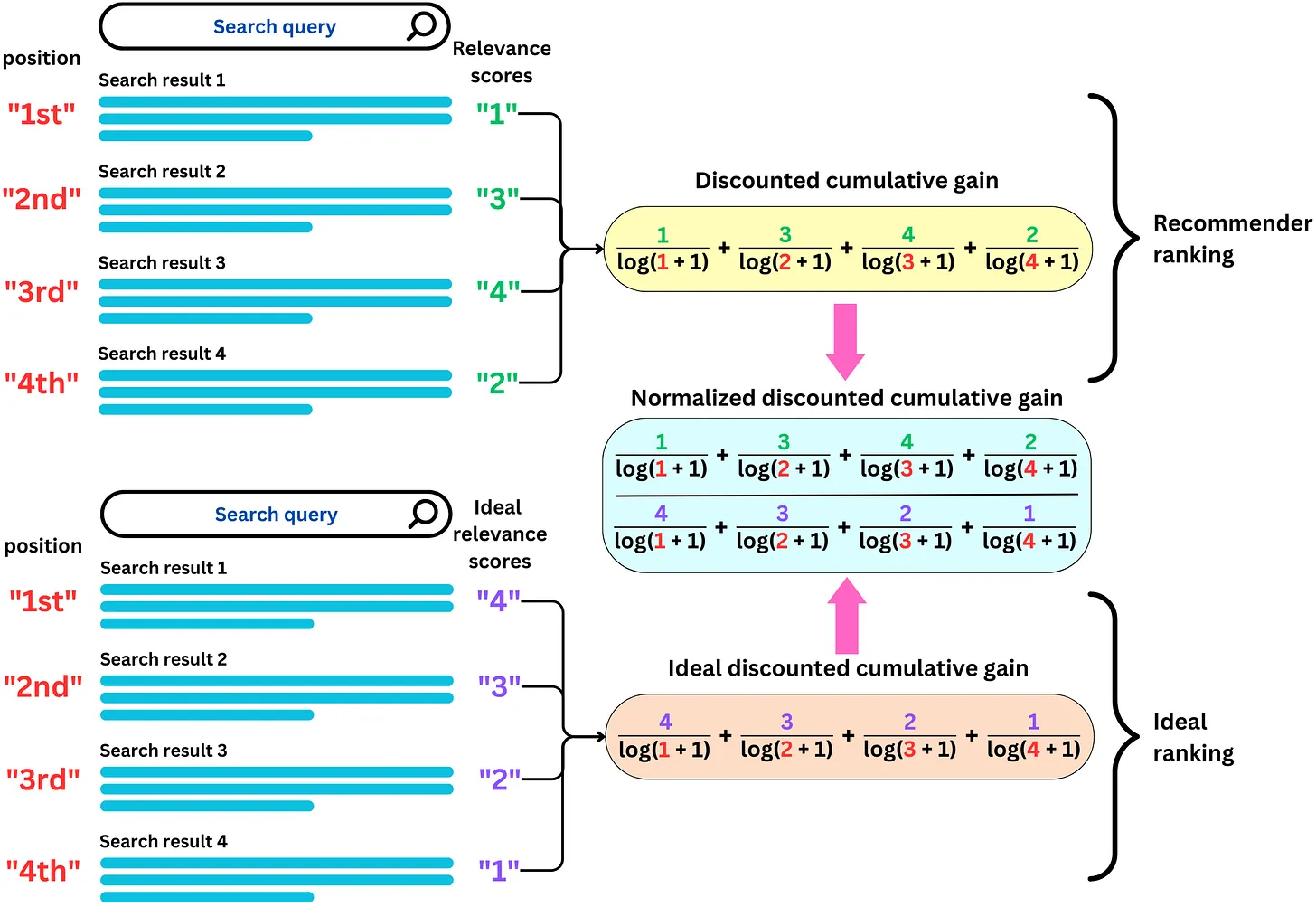
  • Discounted Cumulative Gain (DCG) tại vị trí K được tính bằng công thức:

\[ DCG@K = \sum_{i=1}^{K} \frac{2^{\text{rel}_i} - 1}{\log_2(i + 1)} \]

  • Normalized DCG (NDCG) tại vị trí K được tính bằng công thức:

\[ NDCG@K = \frac{DCG@K}{IDCG@K} \]

Trong đó:

  • \(\text{rel}_i\) là mức độ liên quan của mục ở vị trí i.

  • IDCG@K là giá trị DCG cao nhất có thể đạt được (Ideal DCG) tại vị trí K. (ta sắp xếp lại item theo thứ tự trong recommended list theo có điểm số relevant score cao nhất đến thấp nhất)

Lưu Ý

  • NDCG cân nhắc cả thứ hạng và mức độ liên quan, do đó, nó là một chỉ số toàn diện hơn so với Precision và Recall.

  • Giá trị NDCG có thể nằm trong khoảng từ 0 đến 1, với 1 là tốt nhất, cho thấy danh sách đề xuất đạt chất lượng tối ưu.

import numpy as np # type: ignore

def dcg_at_k(recommended_items, relevant_items, k):
    dcg = 0.0
    for i in range(k):
        # for simple example : mask the relevant score is 1 and the non-relevant score is 0
        rel_i = 1 if recommended_items[i] in relevant_items else 0
        dcg += (2**rel_i - 1) / np.log2(i + 2)
    return dcg

def ndcg_at_k(recommended_items, relevant_items, k):
    dcg_max = dcg_at_k(sorted(relevant_items, reverse=True), relevant_items, k)
    dcg = dcg_at_k(recommended_items, relevant_items, k)
    return dcg / dcg_max if dcg_max > 0 else 0

recommended_items = [1, 2, 3, 4, 5]
relevant_items = [3, 4, 7]
k = 3

ndcg = ndcg_at_k(recommended_items, relevant_items, k)
print(f"NDCG@{k}: {ndcg}")

NDCG@3: 0.23463936301137822

2.5.6.1.3.7. Hit-Rate#

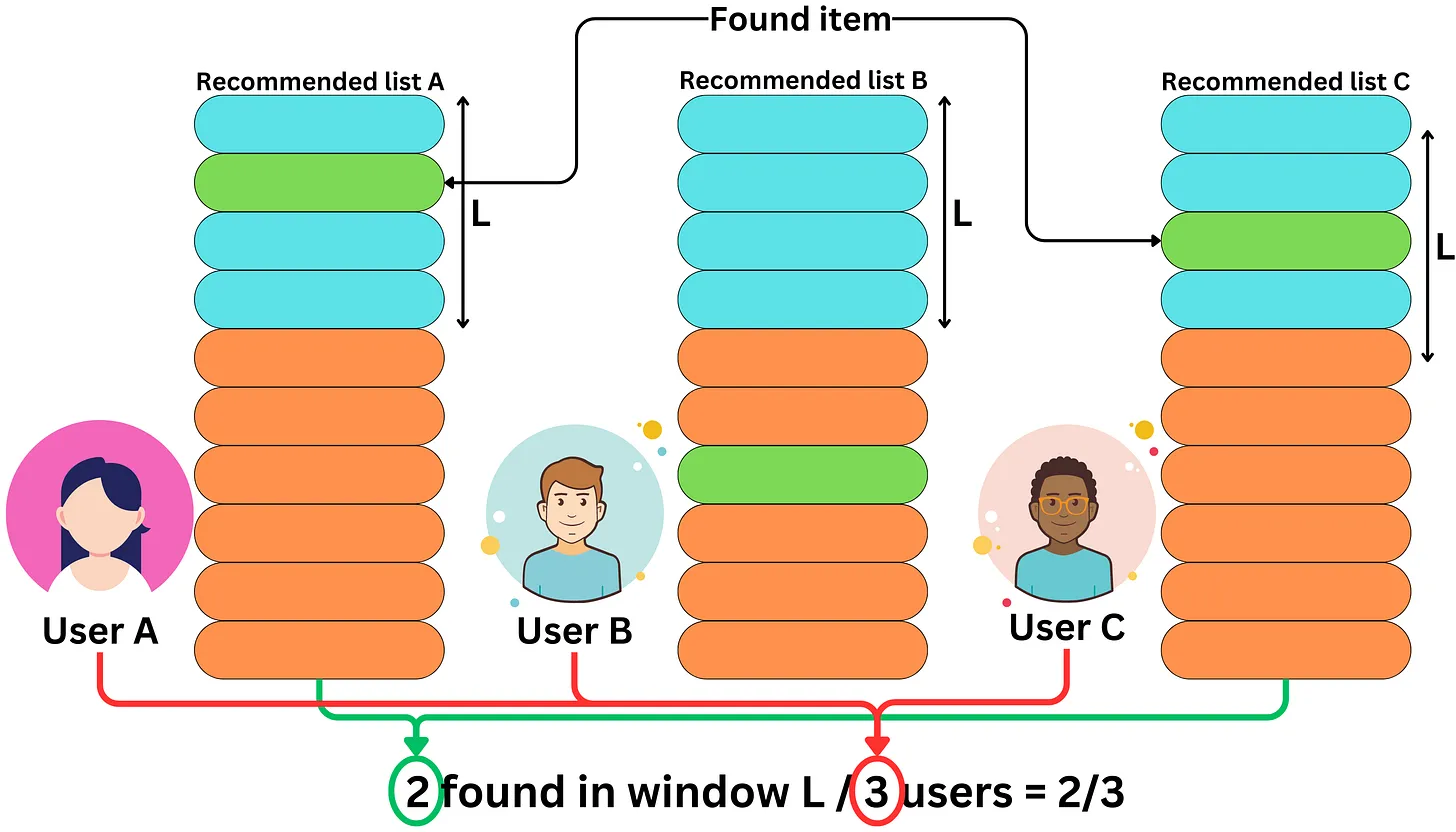
Định Nghĩa và Cách Đánh Giá

Hit-Rate là tỷ lệ phần trăm các phiên (session) hoặc người dùng mà hệ thống recommendation đưa ra ít nhất một mục được người dùng lựa chọn. Chỉ số này giúp đo lường khả năng của hệ thống trong việc cung cấp ít nhất một đề xuất có thể được chọn.

Khi Nào Sử Dụng

Hit-Rate được sử dụng để đo lường sự thành công của hệ thống recommendation trên toàn bộ tập người dùng, đặc biệt là khi mục tiêu là tạo ra các đề xuất có khả năng được lựa chọn cao. Đây là chỉ số hữu ích để đánh giá khả năng của hệ thống trong việc tạo ra ít nhất một gợi ý có giá trị cho người dùng.

Công Thức

Hit-Rate được tính bằng công thức:

\[ \text{Hit-Rate} = \frac{\text{Số lượng người dùng có ít nhất một gợi ý được chọn}}{\text{Tổng số người dùng}} \]

Trong đó:

  • Số lượng người dùng có ít nhất một gợi ý được chọn là số lượng người dùng mà ít nhất một mục trong danh sách gợi ý của hệ thống đã được chọn.

  • Tổng số người dùng là số lượng toàn bộ người dùng trong tập dữ liệu.

Lưu Ý

  • Hit-Rate chỉ đánh giá việc có ít nhất một mục được chọn, không xét đến số lượng và chất lượng của các mục đó.

  • Chỉ số này rất hữu ích khi bạn muốn đánh giá khả năng tổng thể của hệ thống recommendation trong việc tạo ra các gợi ý có thể được chọn.

Trong nhiều trường hợp, kích thước K vô cùng quan trọng

def hit_rate(recommendations, true_interactions):
    hits = 0
    for recommended_items, actual_items in zip(recommendations, true_interactions):
        if any(item in actual_items for item in recommended_items):
            hits += 1
    return hits / len(recommendations)

recommendations = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
true_interactions = [[3], [10], [7]]

hit_rate_score = hit_rate(recommendations, true_interactions)
print(f"Hit-Rate: {hit_rate_score}")

Hit-Rate: 0.6666666666666666

2.5.6.1.4. System monitoring metrics#

  1. Coverage

  2. Novelty

  3. Serendipity

Coverage, Novelty, Serendipity: Là các chỉ số đánh giá tính đa dạng, khả năng khám phá và sự bất ngờ trong các đề xuất của hệ thống, đóng vai trò quan trọng trong việc nâng cao trải nghiệm người dùng.

2.5.6.1.4.1. Coverage#

Định Nghĩa và Cách Đánh Giá

Coverage là chỉ số đo lường tỷ lệ các mục có sẵn trong hệ thống được hệ thống recommendation system đề xuất. Coverage thể hiện mức độ đa dạng của các mục được đề xuất, cho thấy khả năng của hệ thống trong việc giới thiệu nhiều loại mục khác nhau.

Khi Nào Sử Dụng

Coverage hữu ích khi cần đánh giá tính đa dạng và khả năng bao phủ của hệ thống recommendation system. Chỉ số này giúp đo lường phạm vi mà hệ thống có thể khám phá và đề xuất các mục khác nhau, làm tăng sự phong phú của trải nghiệm người dùng.

Công Thức

Coverage được tính bằng công thức:

\[ Coverage = \frac{|\text{Items Recommended}|}{|\text{Total Items}|} \]

Trong đó:

  • Items Recommended là số lượng mục được hệ thống đề xuất.

  • Total Items là tổng số mục có sẵn trong hệ thống.

Lưu Ý

  • Coverage không đánh giá trực tiếp chất lượng của các mục được đề xuất mà chỉ đánh giá phạm vi bao phủ của hệ thống.

  • Một hệ thống có Coverage cao nhưng chất lượng thấp có thể gây khó chịu cho người dùng, vì số lượng lớn các mục không đảm bảo chúng đều là những gợi ý tốt hoặc phù hợp.

def coverage(recommended_items, all_items):
    unique_recommended = set(recommended_items)
    return len(unique_recommended) / len(all_items)

recommended_items = [1, 2, 3, 1, 2, 4]
all_items = [1, 2, 3, 4, 5, 6, 7]

coverage_ratio = coverage(recommended_items, all_items)
print(f"Coverage: {coverage_ratio}")

Coverage: 0.5714285714285714

2.5.6.1.4.2. Novelty#

Định Nghĩa và Cách Đánh Giá

Novelty là chỉ số đánh giá mức độ mới lạ của các mục được đề xuất đối với người dùng, dựa trên sự phổ biến hoặc tần suất các mục này đã từng được đề xuất trước đó. Novelty giúp đo lường khả năng của hệ thống trong việc giới thiệu các mục chưa phổ biến hoặc ít được biết đến, từ đó làm phong phú trải nghiệm của người dùng.

Khi Nào Sử Dụng

Novelty quan trọng khi cần tối ưu hóa để đưa ra các đề xuất mới lạ, chưa từng xuất hiện nhiều trước đó, giúp người dùng khám phá các mục mới và khác biệt. Đây là chỉ số hữu ích khi mục tiêu là tạo ra sự bất ngờ và khám phá cho người dùng.

Công Thức

Một cách tiếp cận đơn giản để tính Novelty là:

\[ Novelty = \frac{1}{|\text{R}|} \sum_{i \in \text{R}} \frac{1}{\log_2(1 + \text{popularity}(i))} \]

Trong đó:

  • popularity(i) là độ phổ biến của mục i trong hệ thống.

  • R là tập các mục được đề xuất.

Lưu Ý

  • Novelty cần cân bằng với các chỉ số khác như Precision để đảm bảo rằng các mục mới lạ vẫn có chất lượng tốt và đáp ứng nhu cầu của người dùng.

  • Hệ thống với Novelty cao có thể gặp khó khăn trong việc duy trì sự quan tâm của người dùng nếu các mục được đề xuất quá xa lạ hoặc không phù hợp với sở thích của họ.

def novelty(recommended_items, item_popularity):
    novelty_score = 0.0
    for item in recommended_items:
        novelty_score += 1 / np.log2(1 + item_popularity.get(item, 1))
    return novelty_score / len(recommended_items)

recommended_items = [1, 2, 3, 4, 5]
item_popularity = {1: 100, 2: 50, 3: 10, 4: 5, 5: 1}

novelty_score = novelty(recommended_items, item_popularity)
print(f"Novelty: {novelty_score}")

Novelty: 0.4004799102329999

2.5.6.1.4.3. Serendipity#

Định Nghĩa và Cách Đánh Giá

Serendipity đánh giá mức độ bất ngờ và thú vị của các mục được đề xuất mà người dùng không mong đợi nhưng vẫn có thể thích. Chỉ số này giúp tạo ra trải nghiệm tốt hơn cho người dùng bằng cách giới thiệu các mục không ngờ tới nhưng vẫn phù hợp và có giá trị.

Khi Nào Sử Dụng

Serendipity rất quan trọng khi muốn hệ thống không chỉ đưa ra các mục liên quan mà còn mang lại sự ngạc nhiên thú vị cho người dùng. Chỉ số này giúp làm phong phú trải nghiệm người dùng bằng cách giới thiệu các đề xuất độc đáo và khác biệt, tạo sự hấp dẫn và sự mới mẻ.

Công Thức

Serendipity thường được đo lường bằng cách kết hợp giữa độ mới lạ và mức độ liên quan. Tuy nhiên, không có công thức cụ thể phổ quát cho Serendipity, vì nó thường phụ thuộc vào cách định nghĩa và yêu cầu cụ thể của từng hệ thống recommendation.

Lưu Ý

  • Serendipity cần được cân bằng với độ chính xác, tránh trường hợp hệ thống đưa ra các mục quá bất ngờ nhưng không liên quan đến sở thích hoặc nhu cầu của người dùng.

  • Đo lường Serendipity có thể phức tạp vì cần hiểu rõ hành vi và sở thích của người dùng để đảm bảo các mục đề xuất không chỉ bất ngờ mà còn phù hợp và có giá trị.

def serendipity(recommended_items, relevant_items, user_profile):
    surprising_items = set(recommended_items) - set(user_profile)
    relevant_surprising_items = surprising_items & set(relevant_items)
    return len(relevant_surprising_items) / len(recommended_items)

recommended_items = [1, 2, 3, 4, 5]
relevant_items = [3, 4, 7]
user_profile = [1, 2]

serendipity_score = serendipity(recommended_items, relevant_items, user_profile)
print(f"Serendipity: {serendipity_score}")

Serendipity: 0.4
Contents